文章目录:
- 一、常用知识
- 二、常用函数
- STL
- 1. Sort 排序
- 2. 二分查找函数 (STL版)
- 3. Vector (动态数组) 常用操作
- 4. String (字符串)
- 5. Priority Queue (优先队列/堆)
- 6. Map 与 Set (映射与集合)
- 7. 去重 (Unique) 与 全排列
- 内置位运算
- 最大公约数与最小公倍数
- 负数取模
- 向上取整
- 常用数据结构
- 三、理论知识(for 选择题)
- 证明算法正确性
- 分治算法
- 各种渐进符号
- 求解递归式
- (未完成)几种排序
- 图算法相关
- 计算几何相关
- FFT
- 1. 复数单位根(roots of unity)
- 2. DFT:在单位根处的多项式求值
- 3. FFT:用分治快速计算 DFT
- 4. 逆 DFT(inverse DFT)与卷积定理
- 5. 蝶形运算(butterfly)
- 6. 迭代 FFT 与 Bit-reversal
- 字符串相关
- 四、排序与分治
- 五、动态规划
- 装配线调度 ALS
- 钢管切割问题
- 矩阵连乘 MCM
- 最优二叉搜索树 OBST
- 最长上升子序列
- 最长公共子序列
- 最长公共子串
- 01背包问题
- 完全背包问题
- 多重背包问题
- 分组背包问题
- 石子合并(区间DP)
- 六、贪心算法
- 七、图算法
- 八、计算几何
- 九、FFT
- 十、字符串
- 十一、其它常用算法(包括上机中算法)
我的算法资料开源仓库:https://github.com/lixu10/algorithm-template
上课的英文PPT这的看不懂(中文我都不一定看的懂),用AI按章节转成了说人话版(仅保留算法核心部分):算法PPT按章节总结.pdf
自己结合学长板子、AI、自己代码,写了一套非常完整的板子,包含所有课上算法、常用算法等(与这篇文章下面内容相同)。下载:板子ver5.pdf
Recommend:
ACM算法模板(吉林大学).pdf
算法模板.md
C STL超全汇总-2023.12.11.pdf
Acwing代码总结
算法选择题复习.pdf
算法模板 (1).md
模板.pdf
算法板子 - Rainel
C++算法板子积累 - OnlyAR
以下为我自己的代码模板:
[TOC]
一、常用知识
常用框架
#include <bits/stdc++.h> // 万能头文件,包含几乎所有STL
using namespace std;
// 定义简写,手写速度更快
typedef long long ll;
typedef pair<int, int> pii;
#define pb push_back
#define all(x) (x).begin(), (x).end()
#define fi first
#define se second
#define endl '\n' // 避免flush缓冲区,比std::endl快得多int main() {
// 关流同步,C++输入输出提速关键,开启后不要混用cin/cout和scanf/printf
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
// 设置输出浮点数精度(例如保留10位小数)
cout << fixed << setprecision(10);
return 0;
}常用数值
// 【无穷大】
// int型的无穷大,推荐 0x3f3f3f3f (约10^9)
// 好处:两个INF相加不会溢出int,且可以用memset赋值
const int INF = 0x3f3f3f3f;
// long long型的无穷大,推荐 4e18 (2^62左右)
const ll LLINF = 4e18;
// 【数学常量】
const double PI = acos(-1.0);
const double EPS = 1e-9; // 浮点数比较误差
// 【取模】
const int MOD = 1e9 + 7;
// const int MOD = 998244353; // 另一个常见模数memset
int dp[1005];
// 赋为 0
memset(dp, 0, sizeof(dp));
// 赋为 -1
memset(dp, -1, sizeof(dp));
// 赋为无穷大 (0x3f3f3f3f) -> 常用求最小值问题
memset(dp, 0x3f, sizeof(dp));
// 赋为极小值 (0xc0c0c0c0, 约 -10^9) -> 常用求最大值问题
memset(dp, 0xc0, sizeof(dp)); 数据范围
int: 范围 $\approx \pm 2 \times 10^9$。
- 注意:如果题目结果可能达到 $10^{10}$ 以上(如累加和、大数相乘),必须用
long long。
long long: 范围 $\approx \pm 9 \times 10^{18}$。
unsigned long long: 范围 $\approx 1.8 \times 10^{19}$ (仅正数,自然溢出哈希常用)。
数组大小限制:
- 一般题目限制 256MB。
int数组最大开到约6e7(6000万)。long long数组最大开到约3e7(3000万)。- 通常二维数组
dp[5000][5000]是极限。
时间复杂度
C++ 一般 1秒 能跑 $10^8$ (一亿) 次基本运算。根据数据规模 $N$ 选择算法:
| 数据规模 N | 允许的时间复杂度 | 常见算法 |
|---|---|---|
| $N \le 20$ | $O(2^N)$ 或 $O(N!)$ | 状态压缩DP、DFS爆搜 |
| $N \le 100$ | $O(N^4)$ | Floyd、复杂DP |
| $N \le 500$ | $O(N^3)$ | Floyd、区间DP、高斯消元 |
| $N \le 2000$ | $O(N^2)$ | 冒泡/选择排序、基础DP、Dijkstra(朴素) |
| $N \le 10^5$ | $O(N \log N)$ | sort、堆、线段树、二分、Dijkstra(堆优化) |
| $N \le 10^6$ | $O(N)$ | 并查集、KMP、双指针、线性筛、差分/前缀和 |
| $N \le 10^7$ | $O(N)$ | 必须常数极小的线性算法 |
| $N > 10^9$ | $O(\sqrt{N})$ 或 $O(\log N)$ | 数论分块、快速幂、GCD |
二、常用函数
STL
vector 变长数组,倍增的思想
size() 返回元素个数
empty() 返回是否为空
clear() 清空
front()/back()
push_back() / pop_back()
begin() / end()
[]
支持比较运算,按字典序
pair<int, int>
first, 第一个元
second, 第二个元素
支持比较运算,以first为第一关键字,以second为第二关键字(字典序)
string,字符串
size()/length() 返回字符串长度
empty()
clear()
substr(起始下标,(子串长度)) 返回子串
c_str() 返回字符串所在字符数组的起始地址
queue, 队列
size()
empty()
push() 向队尾插入一个元素
front() 返回队头元素
back() 返回队尾元素
pop() 弹出队头元素
priority_queue, 优先队列,默认是大根堆
size()
empty()
push() 插入一个元素
top() 返回堆顶元素
pop() 弹出堆顶元素
定义成小根堆的方式:
priority_queue<int, vector<int>, greater<int> > q;
priority_queue<coord, vector<coord>, decltype(&Lcmp)> pq(Lcmp);
bool Lcmp (const coord & c1 , const coord & c2){
return c1 .l < c2.l; }
stack, 栈
size()
empty()
push() 向栈顶插入一个元素
top() 返回栈顶元素
pop() 弹出栈顶元素
deque, 双端队列
size()
empty()
clear()
front()/back()
push_back()/pop_back()
push_front()/pop_front()
begin()/end()
[]
set, map, multiset, multimap, 基于平衡二叉树(红黑树),动态维护有序序列
size()
empty()
clear()
begin()/end()
++, -- 返回前驱和后继,时间复杂度 O(logn)
set/multiset
insert() 插入一个数
find() 查找一个数
count() 返回某一个数的个数
erase()
(1) 输入是一个数x,删除所有x O(k + logn)
(2) 输入一个迭代器,删除这个迭代器
lower_bound() / upper_bound() // 找不到都返回后面
lower_bound(x) 返回大于等于x的最小的数的迭代器
upper_bound(x) 返回大于x的最小的数的迭代器
//123456789递增序列 a < x ,x,x,x,x,x,x < b
// low up
map/multimap
insert() 插入的数是一个pair
erase() 输入的参数是pair或者迭代器
find()
[] 注意multimap不支持此操作。 时间复杂度是 // O(logn)
lower_bound()/upper_bound()
unordered_set, unordered_map,
unordered_multiset, unordered_multimap, 哈希表
和上面类似,增删改查的时间复杂度是 O(1)
不支持 lower_bound()/upper_bound(), 迭代器的++,--
bitset, 圧位
bitset<10000> s;
~, &, |, ^ // 取反, 位和, 位或, 位异或
>>, << // 左右移动
==, !=
[]
count() 返回有多少个1
any() 判断是否至少有一个1
none() 判断是否全为0
set() 把所有位置成1
set(k, v) 将第k位变成v
reset() 把所有位变成0
flip() 等价于~
flip(k) 把第k位取#include<cmath>
pow(2,3)乘方运算
sqrt()
abs()
fmod(3.4,2.1)浮点取模
ceil()向上取整
floor()向下取整
round()四舍五入
cbrt()开三次方
hypot()计算斜边
sin(pi/2)
cos()
tan()
asin()
acos()
atan()
log()
log2()
log10()
#include<algorithm>
fill(intArray,intArray+10,1)
fill1. Sort 排序
包含基础排序、结构体排序、Lambda表达式排序(代码更短)。
#include <algorithm>
#include <vector>
using namespace std;
// 【结构体定义】
struct Node {
int id, score;
};
// 【通用比较函数 cmp】
// 规则:返回 true 表示 a 排在 b 前面
bool cmp(Node a, Node b) {
if (a.score != b.score)
return a.score > b.score; // 分数不同:按分数从大到小(降序)
return a.id < b.id; // 分数相同:按ID从小到大(升序)
}
void solve_sort() {
vector<int> a = {3, 1, 4, 1, 5};
vector<Node> v = {{1, 90}, {2, 95}, {3, 90}};
// 1. 基础升序 (从小到大)
sort(a.begin(), a.end());
// 2. 基础降序 (从大到小)
// 需包含 <functional> 或万能头
sort(a.begin(), a.end(), greater<int>());
// 3. 结构体排序 (使用上面的 cmp 函数)
sort(v.begin(), v.end(), cmp);
// 4. Lambda 表达式排序 (考试偷懒写法,无需写外部cmp函数)
// []内捕获变量,()内参数
sort(v.begin(), v.end(), [](Node a, Node b) {
if (a.score != b.score) return a.score > b.score;
return a.id < b.id;
});
}2. 二分查找函数 (STL版)
前提: 数组/容器必须是有序的(通常先 sort)。
返回值: 返回的是迭代器 (iterator),减去 .begin() 才是下标。
void solve_binary_search() {
vector<int> a = {1, 2, 4, 4, 4, 6, 8};
// 目标值
int x = 4;
// 1. lower_bound: 查找第一个 >= x 的元素位置
// 如果所有数都 < x,返回 a.end()
int pos1 = lower_bound(a.begin(), a.end(), x) - a.begin();
// pos1 = 2 (对应第一个4)
// 2. upper_bound: 查找第一个 > x 的元素位置
int pos2 = upper_bound(a.begin(), a.end(), x) - a.begin();
// pos2 = 5 (对应数字6)
// 【常见应用】
// x 出现的次数
int count = pos2 - pos1;
// 判断 x 是否存在
bool exist = (pos1 != a.size() && a[pos1] == x);
}3. Vector (动态数组) 常用操作
vector<int> v;
// 1. 插入与删除
v.push_back(10); // 尾插
v.pop_back(); // 尾删
// 2. 初始化大小与初值
// 开一个大小为 n,全为 -1 的数组
vector<int> v2(n, -1);
// 3. 调整大小 (重要)
// 改变数组长度,新增加的部分默认补0
v.resize(100);
// 4. 清空
v.clear(); // size变0,capacity不变
a.front(); // 第一个数
a.back(); // 第二个数
a.size(); // 返回数据个数
a.begin(); // 返回数组首地址迭代器
a.end(); // 返回数组尾地址迭代器(最后一个元素的下一个位置)
a.empty(); // 是否为空
a.assigm(beg, end); // 将另一个容器[x.begin(), x.end()]拷贝到a里面
a.pop_back(); // 删除最后一个元素
a.push_back(element); // 最后面加一个元素
a.insert(pos, x); // 向任意迭代器pos插入一个元素x
a.resize(n, v); // 改变数组大小为n,且赋值为v
a.erase(first, last); // 删除[first, last)之间的元素4. String (字符串)
string s = "Hello World";
// 1. 截取子串 (起始下标, 长度)
// 常用!注意第二个参数是长度,不是结束下标
string sub = s.substr(6, 5); // "World"
// 2. 查找子串
// 返回第一次出现的下标,找不到返回 string::npos
int pos = s.find("World");
if (pos != string::npos) { /* 找到了 */ }
// 3. 数字转字符串 / 字符串转数字
string s_num = to_string(123); // "123"
int num = stoi("123"); // 123 (long long用 stoll)
// 4. 字典序比较
// 直接使用 < > == 即可
if ("abc" < "abd") { /* true */ }5. Priority Queue (优先队列/堆)
注意: 默认是大根堆(大的在堆顶)。
// 1. 大根堆 (默认)
priority_queue<int> q_max;
q_max.push(5);
q_max.push(1);
int top_val = q_max.top(); // 5
q_max.pop(); // 弹出堆顶
// 2. 小根堆 (写法很长,容易忘,建议背)
// 参数:类型, 容器(vector), 比较器(greater)
priority_queue<int, vector<int>, greater<int>> q_min;
// 3. 结构体堆 (需重载 < 运算符)
struct Node {
int x;
// 重载 < 符号,大根堆默认逻辑:return 左 < 右
// 如果想让 x 小的在堆顶(变相小根堆),这里反着写 return a.x > x;
bool operator < (const Node& a) const {
return x < a.x;
}
};
priority_queue<Node> q_struct;排序规则:
priority_queue<int, vector<int>, greater<int>> q; // 小顶堆- 第一个参数:储存数据类型
- 第二个参数:存放底层数据结构堆的容器,改
<int>里面的int就可以 - 第三个参数:比较方法,自带的有
less<int>和greater<int>(分别大顶堆、小顶堆)。 - 无比较参数默认为大顶堆。
主要是排序比较函数的写法。比较函数返回1代表不满足规则,返回0代表不需要改变顺序。所以比较函数和正常的想法可能是反着的,比如return小于号得到的是一个大顶堆。
定义里面的cmp是一个struct结构体。有以下的定义方法:
// 单独定义一个比较结构体
struct cmp{
bool operator()(const Point& a, const Point$ b){
return a.x < b.x;
}
}
priority_queue<Point, vector<Point>, cmp> q; // 对x的大顶堆
// 或者直接在数据的结构体里面写
struct Point {
int x, y;
friend bool operator < (Point a, Point b) {//为两个结构体参数,结构体调用一定要写上friend
return a.x < b.x; //大根堆,按x从小到大排,x大的在堆顶
}
}
priority_queue<Point> q; // 相当于给结构体写了一个自带比较方法对于pair类型,先对first进行降序排序,再对second进行降序排序。
6. Map 与 Set (映射与集合)
map/set: 基于红黑树,有序,操作 $O(\log N)$。unordered_map/unordered_set: 基于哈希表,无序,操作 $O(1)$,但容易被卡常或退化,考试求稳建议用 map。
// 1. Map (键值对 Key-Value)
map<string, int> mp;
mp["apple"] = 5;
mp["banana"]++; // 默认初值为0,可以直接++
// 遍历 (C++11)
for (auto p : mp) {
// p.first 是 Key, p.second 是 Value
cout << p.first << " " << p.second << endl;
}
// 查找 key 是否存在
if (mp.count("apple")) { /* 存在 */ }
// 2. Set (自动去重 + 排序)
set<int> st;
st.insert(5);
st.insert(1);
st.insert(5); // 重复插入无效
// 此时 st 内部为 {1, 5}
// 获取首元素 (最小值)
int min_val = *st.begin();
// 获取末元素 (最大值)
int max_val = *st.rbegin();7. 去重 (Unique) 与 全排列
vector<int> a = {1, 1, 2, 2, 3};
// 1. 数组去重 (必须先排序!)
sort(a.begin(), a.end());
// unique 将重复元素移到末尾,返回新末尾迭代器,erase 删除后面垃圾
a.erase(unique(a.begin(), a.end()), a.end());
// 结果: {1, 2, 3}
// 2. 下一个全排列 (字典序)
// 比如 {1, 2, 3} -> {1, 3, 2}
vector<int> p = {1, 2, 3};
do {
// 处理当前排列 p
for(int x : p) cout << x << " ";
cout << endl;
} while (next_permutation(p.begin(), p.end()));
// 循环结束条件是:已经是最大字典序 (3, 2, 1)内置位运算
注意:long long 版本要在函数名后加 ll,如 __builtin_popcountll
int x = 12; // 二进制 1100
// 1. 计算二进制中 1 的个数
int cnt = __builtin_popcount(x); // 结果 2
// 2. 计算二进制中前导 0 的个数 (clz = count leading zeros)
int lead = __builtin_clz(x);
// 3. 计算二进制中末尾 0 的个数 (ctz = count trailing zeros)
int trail = __builtin_ctz(x);
// 4. 计算二进制最后一位 1 所在位置 (1-based), x=0返回0
int idx = __builtin_ffs(x);
最大公约数与最小公倍数
int g = __gcd(a, b); // 内置函数
int l = (a * b) / g; // 注意 a*b 可能溢出,建议 a/g*b辗转相除:
typedef long long ll;
ll gcd(ll a, ll b) {
return b ? gcd(b, a % b) : a;
}负数取模
C++中负数取模结果可能是负数(如 -5 % 3 = -2)。如果需要正余数:
int ans = (a % MOD + MOD) % MOD;向上取整
整数 a / b 默认向下取整。如果需要向上取整 ceil(a/b):
int ans = (a + b - 1) / b;常用数据结构
二分查找
template <typename T>
int binary_search(const T* array, int n, T value) {
int left = 0;
int right = n - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (array[mid] == value) {
return mid;
} else if (array[mid] < value) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1;
}并查集
int fa[maxn],size[maxn]; // 祖父节点和大小节点,若fa[i]==i,说明i是这个集合的根
inline void init(int n) // 初始化,每个节点是一个集合
{
for (int i = 1; i <= n; ++i){
fa[i] = i;
size[i] = 1;
}
}
int find(int x) // 查找x节点的集合的根,同时进行路径压缩
{
return x == fa[x] ? x : (fa[x] = find(fa[x]));
}
inline void merge(int i, int j) // 对i节点和j节点进行合并
{
size[find(j)] += size[find(i)];
fa[find(i)] = find(j);
}树状数组(前缀和)
struct Bit {
#define Maxn 1000100
long long val[Maxn];
inline long long lowbit(int x) {return x & -x;} // 最低位1
inline void add(int x, long long v) {while (x < Maxn) {val[x] += v; x += lowbit(x);}} // x位添加v
inline long long ask(int x) {int res = 0; while (x) {res += val[x]; x -= lowbit(x);} return res;} // 返回x位前缀和
inline long long query(int l, int r) {return ask(r) - ask(l - 1);} // 返回[l, r]区间和
} bit;堆
第k小堆
struct Priority_Queue { // 本质是用两个堆存储
int k;
priority_queue<int> q1; // 大根堆,当前集合中最小的 k-1 个元素
priority_queue<int, vector<int>, greater<int> > q2; // 小根堆,保存剩下的所有元素
Priority_Queue() { }
Priority_Queue(int _k) : k(_k) {} // 构造方法,应该用这个
void push(int v) {
q1.push(v);
while (q1.size() >= k) q2.push(q1.top()), q1.pop();
}
void pop() {
if (!q2.empty()) q2.pop();
else if(!q1.empty()) q1.pop();
}
int top() { // 返回当前第k小
if (!q2.empty()) return q2.top();
else if(!q1.empty()) return q1.top();
else return -1;
}
};使用方法:
Priority_Queue pq(3); // 维护第 3 小
pq.push(5);
pq.push(1);
pq.push(7);
// 此时 pq.top() = 当前第 3 小可删除堆
struct p{
int data;
int k;
};
struct H{
#define N 1000000+5
#define type p
type Heap[N];
int HeapSize = 0;
int cmp(const type &a,const type &b){
return a.data<=b.data;
}
void swap(type arr[], int i, int j){
type temp;
temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
void ShiftDown(int i){
int cur = i;
while(cur<=HeapSize){
int left = cur<<1;
int right = left + 1;
int min = cur;
if(left<=HeapSize&&cmp(Heap[left],Heap[min])) min = left;
if(right<=HeapSize&&cmp(Heap[right],Heap[min])) min = right;
if(min==cur) return;
else{
swap(Heap,cur,min);
cur = min;
}
}
}
void ShiftUp(int i){
int cur = i;
while(cur>1){
int parent = cur>>1;
if(!cmp(Heap[parent],Heap[cur])){
swap(Heap,parent,cur);
cur = parent;
}
else return;
}
}
void push(type num){
Heap[++HeapSize] = num;
ShiftUp(HeapSize);
}
void pop(){
if(HeapSize<=0) return ;
Heap[1] = Heap[HeapSize--];
ShiftDown(1);
}
// 删除第k个元素
void del(int k){
if(HeapSize<=0) return;
Heap[k] = Heap[HeapSize--];
ShiftDown(k);
ShiftUp(k);
}
// 修改第k个元素
void repl(int k,type num){
if(HeapSize<k) return;
Heap[k] = num;
ShiftDown(k);
ShiftUp(k);
}
type top(){
return Heap[1];
}
};三、理论知识(for 选择题)
证明算法正确性
当证明算法的正确性时,书中给出了需要证明的三条性质:
- 初始化: 循环的第一次迭代之前,它为真;
- 保持: 如果循环的某次迭代之前它为真,那么下次迭代之前它仍然为真;
- 终止: 在循环终止时,不变是为我们提供了一个有用的性质,该性质有助于证明算法是正确的。
下面用插入算法举例,证明插入算法的正确性:
- 初始化: 当第一次迭代之前(插入算法从
j = 2开始循环),子数组仅有单个元素A[1]组成,一个元素当然是已经排好序的了,那么为真; - 保持: 每次插入元素时,从
j-1到1循环,把大于A[j]的元素往后移一位,直到找到A[j]的合适位置(记为k),那么将A[j]的值插入该元素,那么从[1,k-1]和[k+1,j-1]均为排好序的,A[j]大于等于左边,小于右边,总体也是排好的,所以也为真; - 终止: 循环终止的条件为
j > A.length,子数组A[1..n]由原来的A[1..n]组成,但是是排好序的。所以算法正确。
分治算法
分治算法在本质是递归的,每层递归有三个步骤:
- 分解原问题为子问题,降低规模;
- 递归地解决这些子问题;
- 合并这些问题的解为原问题的解。
下面给出分治算法的分析方法,按照上面的递归步骤:假设 T(n) 是规模为 n 的一个问题的运行时间。若问题规模足够小,如对某个常量 c ,$ n \leq c$ ,则直接求解需要常量时间,我们将其写作 $\Theta(1) $。假设把原问题分解成 a 个子问题,每个子问题的规模是原问题的 $ 1/b$ 。为了解决一个规模为 $n/b$ 的子问题,需要 $ T(n/b)$ 的时间,所以需要 $aT(n/b)$ 的时间来求解 a 个子问题。如果分解问题成子问题需要时间 $D(n)$ ,合并子问题的解成原问题的解需要时间 $C(n) $,那么得到递归式:
各种渐进符号
$\Theta$记号:用来表示算法的运行时间,渐进给出一个函数的上界和下界。
就是对于任意情况,都能找到$c_1$和$c_2$使得$f(n)$能夹在两个之间。称$g(n)$是$f(n)$的一个渐进紧确界。
O记号: 只有一个渐进上界,用来反映最坏情况也是总体的最坏运行时间。
$\Omega$记号: 表示渐进下界,表示无论什么输入,程序的最好情况。
o记号: 表示非渐进紧确的上界,即程序的运行时间一定小于某个数量级。
$\omega$记号: 表示非渐进紧确的下界。
求解递归式
1. 代入法
代入法本质上就是先猜后证。常见步骤:
- 猜测解的形式
- 用数学归纳法求出解中的常数,并证明解是正确的
2. 递归树法
递归树是我们把程序的递归画成一棵树的结构。递归树中,每个结点表示一个单一子问题的代价,子问题对应某次递归函数调用。我们将树中每层中的代价求和,得到每层代价,然后将所有层的代价求和,得到所有层次的总代价。
例如:求解递归式 $T(n) = 3T(\lfloor n/4 \rfloor) + \Theta(n^2)$ :
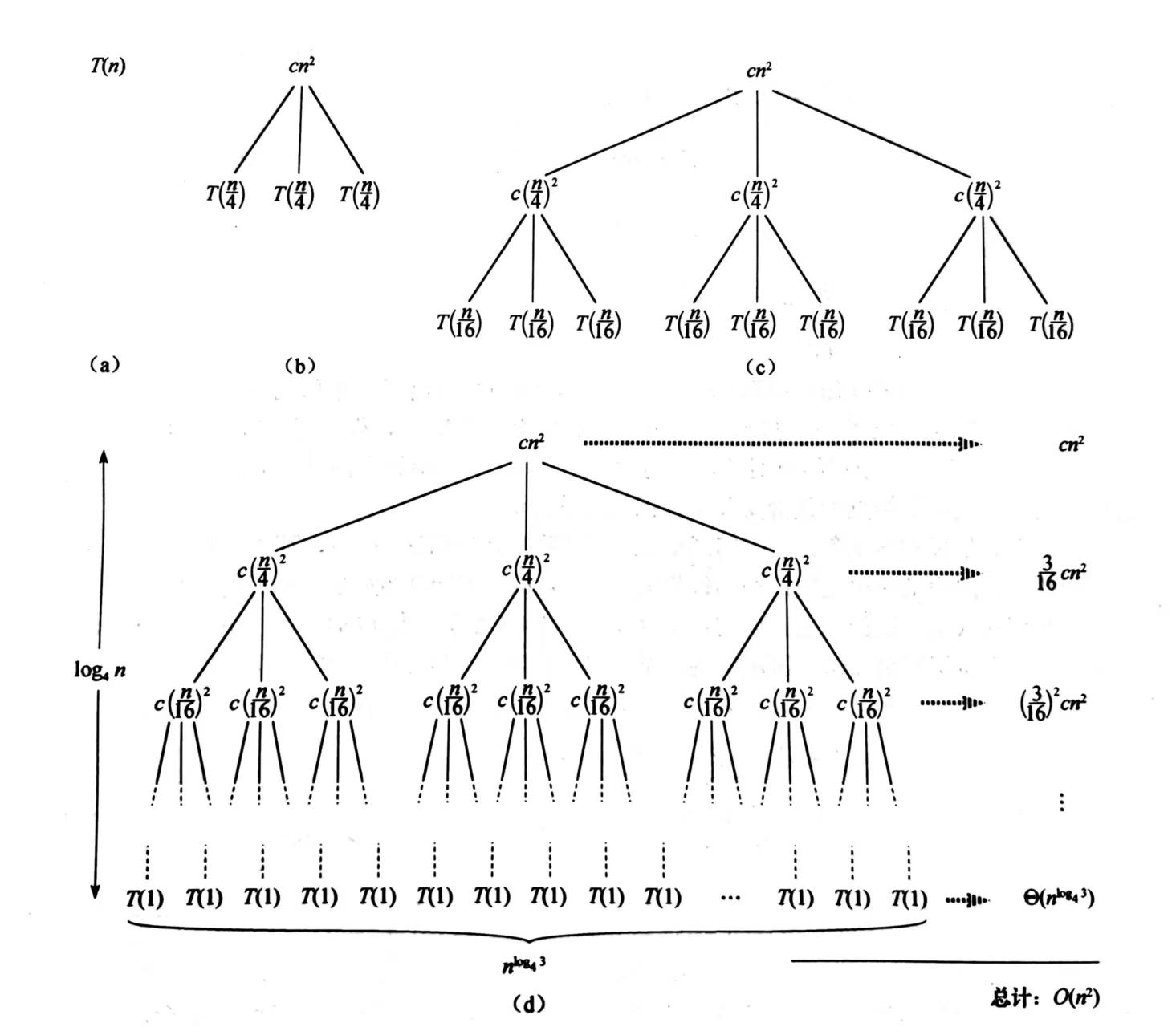
总的代价为:
3. 主定理
主方法可以求解如下形式的递归式:
其中 $a≥1$ 和 $b>1$ 是常数, $f(n)$ 是渐进正函数。
描述的问题是:将规模为n的问题分解为a个子问题,每个子问题的规模为 $n/b$ ,其中 $a$ 和 $b$ 都是正整数。 $a$ 个子问题递归地进行求解,每个花费时间 $ T(n/b)$ 。函数 $f(n)$ 包含问题分解和子问题解合并的代价。
定理 4.1(主定理)
令 $a\geqslant1$ 和 $b>1$ 是常数, $f(n)$ 是一个函数, $T(n)$ 是定义在非负整数上的递归式:
$$ T(n) = aT(n/b) + f(n) $$其中我们将 $n/b$ 解释为 $\lfloor n/b \rfloor$ 或 $\lceil n/b \rceil$ 。那么 $T(n)$ 有如下渐近界:
- 若对某个常数 $\varepsilon>0$ 有 $f(n)=O(n^{\log_b a - \varepsilon})$ ,则 $T(n)=\Theta(n^{\log_b a})$ 。
- 若 $f(n)=\Theta(n^{\log_b a})$ ,则 $T(n)=\Theta(n^{\log_b a} \lg n)$ 。
- 若对某个常数 $\varepsilon>0$ 有 $f(n)=\Omega(n^{\log_b a + \varepsilon})$ ,且对某个常数 $c<1$ 和所有足够大的 $n$ 有 $af(n/b)\leqslant cf(n)$ ,则 $T(n)=\Theta(f(n))$ 。
使用时我们需要先判断属于三种情况之中的哪一种:将函数 $f(n)$ 与函数 $n^{\log_b a}$ 进行比较(比较的是增长规模,即幂次大小):
若函数 $n^{\log_b a}$ 更大,如情况 1,则解为 $T(n)=\Theta(n^{\log_b a})$。若函数 $f(n)$ 更大,如情况 3,则解为 $T(n)=\Theta(f(n))$ 。若两个函数大小相当,如情况 2,则乘上一个对数因子,解为 $T(n)=\Theta(n^{\log_b a} \lg n)=\Theta(f(n)\lg n)$ 。
例如计算递归式:
可得 $a = 7$ , $b = 2$ ,$f(n) = \Theta(n^2)$ ,所以 $n^{\log_b a} = n^{\log_2 7}$ ,所以 $\log_2 7 > 2.80 > 2$ ,所以应用情况1,得出解 $T(n) = \Theta(n^{lg7})$ 。
(未完成)几种排序
图算法相关
1. 广度优先搜索 BFS
从一个起点 $s$ 出发,把从 $s$ 能到达的所有点按距离一圈一圈地找出来。对无权图(或者所有边权都一样,比如都看作长度 1),BFS 找到的就是从 $s$ 到其他点的最短边数路径。
- 使用一个队列 $Q$,“先进先出”。
搜索顺序:
- 先访问所有距离 $s$ 为 1 的点;
- 再访问所有距离为 2 的点;
- ……
BFS 的时间复杂度(邻接表)是
$$ O(|V|+|E|) $$
2. 深度优先搜索 DFS
从一个顶点出发,一路沿着一条路径走到底,走不动再回溯到分叉点,换一条路继续。核心思想是递归/栈。
对每个顶点维护:
- 颜色:WHITE / GRAY / BLACK
- 发现时间 $d[v]$:第一次递归到这个点的时间戳
- 完成时间 $f[v]$:从这个点出发的所有邻接边都处理完的时间戳
- 前驱 $\pi[v]$
时间戳从 1 开始,每次访问/结束都自增。
括号结构(Parenthesis Theorem):
- 每个顶点对应区间 $[d[u], f[u]]$。
若 $v$ 是 $u$ 的后代,则有嵌套关系:
$$ d[u] < d[v] < f[v] < f[u] $$- 如果 $[d[u],f[u]]$ 和 $[d[v],f[v]]$ 不相交,则 $u,v$ 在 DFS 森林中互不为祖先/后代。
边的分类(只在 DFS 上定义):
- 树边(Tree edges):递归过程中第一次从 $u$ 访问到 $v$ 的边 $(u,v)$。
- 后向边(Back edges):从一个结点指向其祖先的边。
- 前向边(Forward edges):从结点指向其严格后代但不是树边的边。
- 交叉边(Cross edges):既不是祖先-后代关系,又不在同一条 DFS 树路径上的边。
典型应用:
- 用 DFS 看一个有向图是否是 DAG:存在后向边就有环。
- 后面拓扑排序、强连通分量都基于 DFS 的这些性质。
复杂度同BFS。
3. 拓扑排序
在一个有向无环图(DAG)中,找到一种线性顺序,把所有顶点排成列,使得:对每条边 $(u,v)$,$u$ 都出现在 $v$ 前面。
基于DFS: 越先完成的f[v]越大。
- 对图做 DFS,记录所有 $f[v]$。
- 把所有顶点按 $f[v]$ 从大到小排序,得到序列 $L$。
- 输出 $L$ 即拓扑序。
复杂度:$O(|V|+|E|)$
基于BFS: Kahn 算法,核心过程概括如下:
- 找起点:统计所有点的入度,将所有入度为 0 的点放入队列。
删边:
- 取出队头,加入结果序列。
- 遍历该点的出边,将所有下游点的入度减 1。
- 若某点入度减为 0,将其入队。
- 判环:重复上述过程直到队列为空。若结果序列的点数等于总点数,则排序成功;否则图中有环。
4. (强连通分量)
问题:在有向图中,找出所有的强连通分量(SCC)——每个分量里任意两点互相可达。
经典算法(Kosaraju)简述一下(PPT 也隐含是这个):
- 对原图 $G$ 做一次 DFS,记录所有顶点的完成时间 $f[v]$。
- 构造转置图 $G^T$(把每条有向边反向)。
按照第一步得到的完成时间从大到小依次在 $G^T$ 上做 DFS。
- 每次 DFS 遍历到的一整棵树就是一个 SCC。
这样可以把原图“降维”,每个 SCC 收缩成一个点,得到一个 DAG,方便后续分析。
5. 最小生成树
在一个连通无向加权图中,找到一棵包含所有顶点、且无环的子图(树),使得边权之和最小,这棵树叫最小生成树(MST)。
Kruskal 算法
(适合稀疏图)
步骤:
- 把所有边按权重从小到大排序。
- 初始时,每个顶点自己是一个连通分量。
从小到大扫描边 $(u,v)$:
- 如果 $u$ 和 $v$ 目前不在同一分量(加上这条边不会成环),就选这条边加入 MST,并把两个分量合并;
- 否则跳过这条边。
- 选到 $|V|-1$ 条边停止。
常用数据结构:并查集(Disjoint Set / Union-Find)。
Prim 算法
(适合稠密图)
步骤:
- 随便选一个起点 $s$,把它加入生成树集合 $S$。
每一步:
- 从所有“连接 $S$ 与 $V\setminus S$ 的边”中,找一条权值最小的 $(u,v)$,其中 $u\in S$,$v\notin S$;
- 把 $v$ 和边 $(u,v)$ 加入生成树集合。
- 重复直到所有顶点都在 $S$ 中。
可以看作是对“连通边界”不断挑最便宜的边,逐渐“长”出一棵 MST。
6. 单源最短路径
从顶点 $u$ 到 $v$ 的最短路径权重定义为:
几类问题:
- 单源最短路径:给定源点 $s$,求 $\delta(s,v)$ 对所有 $v$。
- 单终点最短路径:可以在反向图里做单源。
- 单对最短路径:只关心某一对 $(s,t)$。
- 任意两点最短路径(All-pairs):可以跑 $n$ 次单源,或者用 Floyd–Warshall 等
性质:最优子结构
- 最短路径有最优子结构:一条最短路径中的任意一段子路径,本身也是对应端点间的最短路径。
| 算法 | 允许负权边 | 允许环 | 其它 |
|---|---|---|---|
| Bellman–Ford | ✔ | ✔ | 不能有从源点可达的负权环(无解) |
| DAG + Topo Sort | ✔ | ✖(DAG) | |
| Dijkstra | ✖(必须非负) | ✔ |
(1) Bellman–Ford 算法
- 允许出现负权边。
- 图中可以有环,但不能有从源点可达的负权环,否则“最短路径”没有意义(可以绕环无限减小)。
BF 的特点:
- 是通用算法:只要没有可达负环就能给出正确结果;
- 若存在可达负环,还能检测出来。
核心:松弛操作:
若
则更新:
步骤:
初始化单源:
- 对所有 $v$,$v.d=\infty,\ v.\pi=\text{NIL}$
- $s.d=0$
重复 $|V|-1$ 轮:
- 对图中每条边 $(u,v)\in E$:做一次
relax(u,v)
- 对图中每条边 $(u,v)\in E$:做一次
最后再扫描一遍所有边 $(u,v)$:
- 如果还能满足 $v.d > u.d + w(u,v)$,说明存在可达负环(否则意味着还能变短)。
- 此时“最短路径”不存在,可以直接报错或返回
false。
输出:每个 $v.d$ 和 $v.\pi$。
复杂度:$O(|V|\cdot|E|)$
(2) 基于拓扑排序的最短路(DAG)
这是对有向无环图(DAG)的特殊情况,比 BF 快得多,也能处理负权边。
适用范围
- 图必须是 DAG(有向无环)。
- 边权可以是负数。
典型场景:任务依赖图、流水线、课程先修体系,边的权值是执行时间、延迟等。
算法思想
- 因为没有环,每条从源点出发的路径长度有限且不会“绕圈”。
- 只要按照拓扑序,一次性把所有边松弛一遍,就够了。
步骤:
- 对图做拓扑排序,得到序列 $L$。
- 初始化单源:$s.d=0$,其他 $v.d=\infty$,$\pi=\text{NIL}$。
按拓扑序列从前到后扫描每个顶点 $u$:
- 对每条出边 $(u,v)$ 执行一次
relax(u,v)。
- 对每条出边 $(u,v)$ 执行一次
因为拓扑序保证:到处理 $u$ 时,所有可能到达 $u$ 的路径都已经处理完了,$u.d$ 已经是最短的,所以每条边只需要松弛一次。
复杂度:$O(|V|\cdot|E|)$
(3) Dijkstra 算法
适用范围
- 图可以有环。
- 所有边权必须是非负的:$w(u,v)\ge 0$。
典型案例(PPT 的百度地图例子):
城市道路网,每条路有正长度或正耗时。求从北京到西安的最短路径。
—— 所有边权为距离/时间,非负,适合用 Dijkstra。
算法思想
Dijkstra 维持两个东西:
- 集合 $S$:已经确定最短路径长度的顶点集合。对每个 $u\in S$,$d[u]=\delta(s,u)$。
- 一个最小优先队列 $Q$(通常用最小堆实现):包含 $V\setminus S$ 中的顶点,按当前 $d[v]$ 排序。
大致过程:
初始化:
- 所有顶点 $v$:$d[v]=\infty,\ \pi[v]=\text{NIL}$
- $d[s]=0$
- $S=\varnothing$
- $Q$ 中包含所有顶点(初始键值就是 $d[v]$)
循环直到 $Q$ 为空:
- 从 $Q$ 里取出 $d[u]$ 最小的顶点 $u$(Extract-Min),加入 $S$。
对 $u$ 的每条出边 $(u,v)$:
如果 $v\notin S$ 且
$$ d[v] > d[u] + w(u,v) $$就更新:
$$ d[v]\gets d[u] + w(u,v), \quad v.\pi\gets u $$并在优先队列中降低 $v$ 的键值(Decrease-Key)。
因为边权非负,一旦 $u$ 被从队列中“弹出”,就可以确定 $d[u]$ 已经是全局最短,不会以后再变小(这是 Dijkstra 的关键贪心正确性依据)。
7. 任意两点最短路径
由于时间复杂度高,所以点数、边数一般很少,所以可以都使用邻接矩阵存储。
(1) 矩阵乘法版
先看一条从 $i$ 到 $j$ 的最短路径 $p$(假设 $i\ne j$):
- 在 $p$ 上,设 $j$ 的前驱是 $k$,那么路径可以拆成:
其中:
- $p'$ 是从 $i$ 到 $k$ 的那一段子路径;
- 整条路径的长度:
关键结论:
如果 $p$ 是 $i\to j$ 的最短路径,那么它的任意一段子路径(例如 $i\to k$ 的那段 $p'$)也是 $i\to k$ 的最短路径。
这叫做最优子结构,是很多 DP 算法的基础。
🌟 用“最多 $m$ 条边”的思路来写递推
定义:
如果图中没有负权环,那么任何最短路径的边数都不会超过 $n-1$。
于是有:
接下来要找 $l_{ij}^{(m)}$ 的递推关系。
递推式:
考虑从 $i$ 到 $j$,边数最多为 $m$ 的最短路径。最后一条边一定是某个 $(k,j)$,于是:
- 前面一段 $i\to k$ 最多用 $m-1$ 条边;
- 那段的最短长度是 $l_{ik}^{(m-1)}$;
- 再加上最后一条边的长度 $w_{kj}$。
在所有可能的 $k$ 中取最小,就得到:
初始条件:
$m=0$ 时,没有中间边:
- $l_{ii}^{(0)} = 0$
- $l_{ij}^{(0)} = \infty,\ i\ne j$
这就是一个标准的 DP。
🌟“慢速版”矩阵 DP 算法
设 $L^{(m)}=(l_{ij}^{(m)})$,EXTEND-SHORTEST-PATHS(L, W):
- 输入:上一轮的矩阵 $L^{(m-1)}$ 和权重矩阵 $W$;
- 输出:新的矩阵 $L^{(m)}$;
- 内部就是三重循环,按刚刚的递推式求每个 $l_{ij}^{(m)}$。
然后“慢速版任意两点最短路算法”是:
- $L^{(1)} = W$
对 $m=2,3,\dots,n-1$:
- $L^{(m)} = \text{EXTEND-SHORTEST-PATHS}(L^{(m-1)}, W)$
- 返回 $L^{(n-1)}$ 作为最终的最短路矩阵。
直观理解:
- 第一次只允许最多 1 条边(就是直接边);
- 第二次允许最多 2 条边;
- …
- 最后允许最多 $n-1$ 条边,就囊括了所有可能长度的简单路径。
运行时间是 $\Theta(n^4)$
(2) Floyd–Warshall 算法
Floyd–Warshall 把注意力放在“路径中允许出现哪些中间点”上。
先定义:
对一条简单路径 $p = \langle v_1, v_2,\dots,v_\ell \rangle$:
- 端点是 $v_1$ 和 $v_\ell$;
- 其他顶点 ${v_2,\dots,v_{\ell-1}}$ 叫做这条路的中间顶点(intermediate vertices)。
然后,对于任意一对顶点 $(i,j)$ 和一个整数 $k$,考虑这样的路径集合:
从 $i$ 到 $j$ 的所有路径中,所有中间顶点都在集合 ${1,2,\dots,k}$ 里。
在这些路径中,取一条最短的,记它的长度为 $d_{ij}^{(k)}$。
特别地:
- 当 $k=0$ 时,不允许任何中间点,所以路径最多只有一条边(直接从 $i$ 到 $j$)。
关键的结构性质:
对 $d_{ij}^{(k)}$ 对应的最短路径 $p$,有两种可能:
路径 $p$ 不经过顶点 $k$:
- 那么 $p$ 的所有中间点都在 ${1,\dots,k-1}$ 里;
所以 $p$ 已经是“只允许中间点在 ${1,\dots,k-1}$ 的最短路”,也就是:
$$ d_{ij}^{(k)} = d_{ij}^{(k-1)} $$
路径 $p$ 经过顶点 $k$:
那么 $p$ 可以拆成两段:
$$ p = p_1 + p_2 $$其中
$p_1$ 是 $i\to k$ 的最短路,中间点在 ${1,\dots,k-1}$;
$p_2$ 是 $k\to j$ 的最短路,中间点也在 ${1,\dots,k-1}$。所以:
$$ d_{ij}^{(k)} = d_{ik}^{(k-1)} + d_{kj}^{(k-1)} $$
综上,两种情况取更小的一个:
初始条件:
- $k=0$ 时,只允许路径长度最多一条边,所以:
由于对任意路径来说,它的中间顶点肯定属于 ${1,\dots,n}$,所以最终的答案是:
这就是 Floyd–Warshall 的 DP 公式。
🌟 Floyd 算法的具体流程
伪代码 FLOYD-WARSHALL(W),可以用自然语言描述如下:
- 初始化:$D^{(0)} = W$;
对 $k$ 从 $1$ 到 $n$:
- 构造一个新矩阵 $D^{(k)}$;
对所有 $i,j$:按公式
$$ d_{ij}^{(k)} = \min \big( d_{ij}^{(k-1)},\ d_{ik}^{(k-1)} + d_{kj}^{(k-1)} \big) $$- 也可以原地更新一个数组 $D$,不断覆盖。
- 返回 $D^{(n)}$ 作为最终的最短路矩阵。
直观上:
- 外层循环 $k$:逐渐允许路径中使用更多编号的中间点;
- 内层双循环 $i,j$:用“是否经过 $k$” 来更新 $i \to j$ 的最短路长度。
结论:Floyd–Warshall 算法的时间复杂度是 $\Theta(n^3)$。
🌟前驱矩阵 $\Pi^{(k)}$:构造具体最短路径
为了能输出具体路径,P18 又对 Floyd 定义了一组前驱矩阵:
- $\Pi^{(k)}=(\pi_{ij}^{(k)})$
- $\pi_{ij}^{(k)}$ 表示:在所有中间顶点属于 ${1,\dots,k}$ 的 $i\to j$ 最短路径中,顶点 $j$ 的前驱是谁。
初值($k=0$):
递推($k\ge1$):
若最短路径没有因为允许使用 $k$ 而变短,即
$$ d_{ij}^{(k)} = d_{ij}^{(k-1)} $$那么前驱不变:
$$ \pi_{ij}^{(k)} = \pi_{ij}^{(k-1)} $$若使用 $k$ 可以得到更短的路径:
$$ d_{ij}^{(k)} = d_{ik}^{(k-1)} + d_{kj}^{(k-1)} $$那么从 $i$ 到 $j$ 的最短路是
$i \to k \to j$ 的组合,其中最后一段是“从 $k$ 到 $j$ 的最短路”,
所以 $j$ 的前驱就是那条 $k\to j$ 最短路中的前驱:
$$ \pi_{ij}^{(k)} = \pi_{kj}^{(k-1)} $$
最终的前驱矩阵:
配合 $D=D^{(n)}$,就可以像前面那章一样恢复出所有最短路径。
时间复杂度:$O(n^3)$
8. 最大流
流网络与流的定义
- 边容量 $c(u,v)$;
流 $f(u,v)$ 满足:
$$ 0\le f(u,v)\le c(u,v),\quad \\ \sum_{v} f(v,u) = \sum_{v} f(u,v)\quad (u\ne s,t) $$流的值:
$$ |f| = \sum_v f(s,v) - \sum_v f(v,s) $$
残留容量与残留网络
$$ c_f(u,v) = \begin{cases} c(u,v) - f(u,v), & (u,v)\in E\\ f(v,u), & (v,u)\in E\\ 0, & \text{otherwise} \end{cases} $$在残留网络 $G_f$ 中寻找增广路径。
增广路径与路径残留容量
- 增广路径:$G_f$ 中从 $s$ 到 $t$ 的简单路径 $p$;
残留容量:
$$ c_f(p) = \min\{c_f(u,v):(u,v)\in p\} $$- 沿 $p$ 压入 $c_f(p)$ 的流可增加总流量。
割与最大流–最小割定理
割 $(S,T)$ 的容量:
$$ c(S,T) = \sum_{u\in S,v\in T} c(u,v) $$对任意流 $f$,任意割 $(S,T)$:
$$ |f| = f(S,T) \le c(S,T) $$- 最大流–最小割定理:
最大流值 = 某个最小割的容量;
残留网络中无增广路径 $\Leftrightarrow$ 已经是最大流。
Ford–Fulkerson 方法与 Edmonds–Karp 算法
Ford–Fulkerson:反复在残留网络中找增广路径、压入瓶颈流,直到没有增广路径。
- 初始所有边的流 $f(u,v)=0$。
- 构造残留网络 $G_f$(一开始就是容量网络本身)。
只要在 $G_f$ 中还能找到一条从 $s$ 到 $t$ 的路径 $p$:
计算路径的残留容量:
$$ c_f(p) = \min \{ c_f(u,v) : (u,v)\in p \} $$对路径上的每条边做:
如果是原图中的正向边 $(u,v)\in E$:
$$ f(u,v) \gets f(u,v) + c_f(p) $$如果是残留网络中的反向边 $(u,v)\notin E$,即原图有 $(v,u)$:
$$ f(v,u) \gets f(v,u) - c_f(p) $$
- 当再也找不到增广路径时,当前的 $f$ 就是最大流。
Edmonds–Karp:在 F–F 中规定用 BFS 找最短增广路径,
实现 Edmonds–Karp 时的流程可以概括为:
- 初始化流 $f(u,v)=0$。
反复执行:
- 在当前残留网络 $G_f$ 上,用 BFS 找一条从 $s$ 到 $t$ 的最短路径 $p$;
- 若找不到,结束;
- 否则计算路径瓶颈 $c_f(p)$;
- 沿路径更新原图的流(正向加、反向减)。
- 返回 $f$ 和 $|f|$。
时间复杂度为
$$ O(|V|\cdot|E|^2) $$
最大二分图匹配的流模型
- 二分图 $L,R$;
- 构造 $s\to L$ 和 $R\to t$ 的容量为 1 的边,中间 $L\to R$ 边容量为 1;
- 跑最大流,流值 = 最大匹配大小,流量为 1 的 $L\to R$ 边就是匹配边。
9. 二分图
二分图:有两类顶点 $L$ 和 $R$,边只在 $L$ 与 $R$ 之间。
最大二分匹配问题:在二分图中选出尽可能多的边,使得每个顶点最多只被一条选中的边连接。
对一个二分图 $G=(L\cup R, E)$,构造如下的流网络:
- 新增一个源点 $s$,连向所有左侧顶点 $u\in L$,边 $(s,u)$ 的容量设置为 1。
- 对原二分图中每条边 $(u,v)$,$u\in L, v\in R$,在流网络中保留这条边,容量为 1。
- 新增一个汇点 $t$,让所有右侧顶点 $v\in R$ 通过边 $(v,t)$ 连接到 $t$,容量为 1。
然后在这个流网络上跑 Edmonds–Karp,得到最大流 $f$。
- 对于每条 $u\in L, v\in R$ 间的边,如果 $f(u,v)=1$,就表示我们在匹配中选择了这条边;
- 所有这样的边组成的集合就是一个最大匹配;
- 最大流的值 $|f|$ 就是最大匹配的大小(匹配边条数)。
计算几何相关
1. 线段基本性质
🌟凸组合:
给两点
它们的凸组合是
也就是
几何意义:$p_3$ 就是线段 $p_1p_2$ 上的某一点(含端点)。所有凸组合构成的集合就是线段 $p_1p_2$。
🌟叉积:
把点当作向量,比如
定义二维向量的叉积为矩阵行列式:
几何意义:
- $|p_1\times p_2|$ 等于由 $0,p_1,p_2,p_1+p_2$ 这四个点构成的平行四边形的有符号面积;
号的正负给出方向信息:
- 若 $p_1\times p_2>0$,则相当于从 $p_2$ 旋转到 $p_1$ 是顺时针;
- 若 $p_1\times p_2<0$,则从 $p_2$ 到 $p_1$ 是逆时针;
- 若 $p_1\times p_2=0$,说明两向量共线。
🌟 算法 1:判断一个向量相对另一个是顺时针还是逆时针(Q1)
问题:
已知两条有向线段 $\overrightarrow{p_0p_1}$ 和 $\overrightarrow{p_0p_2}$,问 $\overrightarrow{p_0p_1}$ 是否在 $\overrightarrow{p_0p_2}$ 的顺时针方向?
做法:
把 $p_0$ 平移到原点,相当于看向量:
计算叉积:
- 若 $\vec a\times\vec b>0$:$\overrightarrow{p_0p_1}$ 在 $\overrightarrow{p_0p_2}$ 的顺时针一侧;
- 若 $<0$:在逆时针一侧;
- 若 $=0$:三点共线。
这样只用加减乘和比较,没有除法。
🌟 算法 2:判断三点是左转还是右转(Q2)
问题:
已知三点 $p_0,p_1,p_2$,走 $p_0\to p_1\to p_2$,在 $p_1$ 处是左转、右转还是直走?
PPT 的技巧:还是用叉积,只是换个写法。
考虑向量:
- $\overrightarrow{p_0p_1}$
- $\overrightarrow{p_0p_2}$
计算
- 若结果 $<0$,说明 $\overrightarrow{p_0p_1}$ 相对于 $\overrightarrow{p_0p_2}$ 是逆时针,也就是在 $p_1$ 处左转;
- 若 $>0$,则在 $p_1$ 处右转;
- 若 $=0$,三点共线,既不左转也不右转。
🌟 算法 3:判断两线段是否相交(Q3)
问题:
给线段 $p_1p_2$ 和 $p_3p_4$,判断它们是否相交(包括端点重合、一个端点落在另一段上等所有情况)。
概念:
- 线段 $p_1p_2$ 横跨(straddle)一条直线:
就是 $p_1$ 和 $p_2$ 在这条直线的两侧(叉积一正一负);端点在直线上是边界情况。
结论:两线段相交当且仅当:
- 每一条线段都横跨对方所在的直线;
- 或者,其中一个线段的端点落在另一个线段上(共线特例)。
伪代码 SEGMENTS-INTERSECT:
辅助函数
DIRECTION(p_i,p_j,p_k):计算叉积$$ (p_k-p_i)\times(p_j-p_i) $$给出三点相对方向(>0、<0、=0)。
ON-SEGMENT(p_i,p_j,p_k):已知 $p_k$ 与线段 $p_ip_j$ 共线,
检查 $x_k$ 和 $y_k$ 是否都在 $[x_i,x_j]$、$[y_i,y_j]$ 的区间内,
也就是看 $p_k$ 是否在线段 $p_ip_j$ 内部/端点:$$ \min(x_i,x_j)\le x_k\le\max(x_i,x_j),\ \min(y_i,y_j)\le y_k\le\max(y_i,y_j) $$
主过程
SEGMENTS-INTERSECT(p1,p2,p3,p4):计算
$$ d_1=DIRECTION(p_3,p_4,p_1),\ d_2=DIRECTION(p_3,p_4,p_2) $$$$ d_3=DIRECTION(p_1,p_2,p_3),\ d_4=DIRECTION(p_1,p_2,p_4) $$- 若 $d_1$ 与 $d_2$ 异号 且 $d_3$ 与 $d_4$ 异号,则两段互相横跨,返回
TRUE。 否则检查四个“端点在线段上”的共线特例:
- 若 $d_1=0$ 且
ON-SEGMENT(p3,p4,p1)为真,也返回TRUE; - 类似对 $p_2,p_3,p_4$ 分别检查。
- 若 $d_1=0$ 且
- 否则返回
FALSE。
2. 是否存在相交线段
问题:
输入 $n$ 条线段,只问一句:有没有任何一对线段相交?
不需要找出所有交点,也不关心交点坐标。
如果暴力两两判断,要做 $\binom{n}{2}$ 次,相当于 $O(n^2)$ 次 SEGMENTS-INTERSECT,线段很多时会很慢。
使用经典的扫描线(sweeping)技巧,把时间降到 $O(n\log n)$。
🌟1. 扫描线思想
- 在平面上竖一条从左到右移动的垂直直线(扫描线);
- 扫描线从最左侧开始,慢慢向右扫过所有线段的端点;
- 在某个位置,只关心与扫描线相交的那些线段,把它们按“与扫描线交点的 $y$ 坐标”从下到上排序,放入一个平衡树 $T$ 里。
关键事实:
若有哪两条线段相交,那么当扫描线走到靠近交点的位置时,这两条线段在 $T$ 中必定成为相邻的两条(上下紧挨着)。
所以我们只需要关注每次插入/删除时,某条线段在 $T$ 中的前驱和后继是否与它相交,而不用所有成对检查。
🌟2. 算法 ANY-SEGMENTS-INTERSECT 的步骤
伪代码:
- 建一个空的有序集合 $T$,用于维护“当前穿过扫描线的线段,按 $y$ 顺序”。
- 把所有线段的端点按 $x$ 坐标从小到大排序(左端点在前,同 $x$ 时先处理左端后处理右端;再用 $y$ 打破平局)。
依次扫描每个端点 $p$:
如果 $p$ 是某条线段 $s$ 的左端点:
- 把 $s$ 插入 $T$ 中合适位置(用二分+叉积判断在谁的上面/下面);
找到 $s$ 在 $T$ 中的上邻居
ABOVE(T,s)和下邻居BELOW(T,s),- 若上邻居与 $s$ 相交,或下邻居与 $s$ 相交,则返回
TRUE。
- 若上邻居与 $s$ 相交,或下邻居与 $s$ 相交,则返回
如果 $p$ 是某条线段 $s$ 的右端点:
- 在 $T$ 中找出 $s$ 的上邻居 a、下邻居 b;
- 删除 $s$;
- 如果 a 和 b 都存在,检查它们是否相交;若是,返回
TRUE。
- 如果扫描完所有端点都没发现相交,返回
FALSE。
3. 凸包
给点集 $Q={p_0,p_1,\dots,p_{n-1}}$,它的凸包 $\text{CH}(Q)$ 定义为:
面积最小的一个凸多边形 $P$,使得 $Q$ 中每个点要么在 $P$ 的边界上,要么在 $P$ 内部。
两种经典算法:
- Graham’s scan:$O(n\log n)$;
- Jarvis’s march(gift wrapping):$O(nh)$,$h$ 是凸包顶点个数。
🌟 Graham 扫描算法:用栈 + 左转判断
核心想法:
- 先按“极角”把点排一圈;
然后模拟用橡皮筋绕一圈的过程:
用一个栈 $S$ 存“当前可能是凸包顶点的点”,
每加入一个新点,就看最后两条边在中间点处是否左转:- 左转:说明折线仍然向外鼓,新点进栈;
- 直走或右转:说明栈顶那个点在凸包内部,弹出它,继续检查。
步骤:
设输入点集为 $Q$:
- 找到 $Q$ 中 $y$ 坐标最小的点 $p_0$,若有并列,取最左的。
把其余点按围绕 $p_0$ 的极角从小到大排序,得到序列
$$ \langle p_1,p_2,\dots,p_m\rangle $$若多个点极角相同,只保留距离 $p_0$ 最远的那个。
比较极角也可用叉积实现。初始化栈:
$$ S=\text{[ }p_0,p_1,p_2\text{ ]} $$对 $i=3$ 到 $m$:
设
- $p_{\text{top}}=\text{TOP}(S)$
- $p_{\text{next}}=\text{NEXT-TO-TOP}(S)$
- 当前新点为 $p_i$
当三点 $(p_{\text{next}},p_{\text{top}},p_i)$ 构成的折线在 $p_{\text{top}}$ 处不是左转(即直线或右转)时:
POP(S),把 $p_{\text{top}}$ 从栈中弹出(说明它不在凸包上)。
- 当循环结束(折线在栈顶处变成左转)时,把 $p_i$ push 进栈:
PUSH(p_i,S)。
- 最后栈 $S$ 中从底到顶依次就是凸包顶点,按逆时针顺序。
“是不是左转”的判断,还是用前面说的叉积公式:
- $<0$:左转;
- $\ge0$:非左转(直线或右转)。
复杂度结论:
- 选 $p_0$:$O(n)$;
- 按极角排序:$O(n\log n)$;
- 主循环中,每个点最多压栈一次、弹栈一次,所以总共 $O(n)$。
综合:
$$ T(n)=O(n\log n) $$
🌟Jarvis 包裹算法(gift wrapping)
直观:
- 想象你拿一张硬纸,把它一边贴在最左下角的点 $p_0$,另一边拉到右方;
- 然后慢慢往上旋转,直到纸的边第一次碰到另一点,那点一定是凸包顶点 $p_1$;
- 接着把纸一边固定在 $p_1$,继续旋转找 $p_2$,……
- 这样一圈“包裹”下来,回到 $p_0$ 时就得到整个凸包。
算法步骤:
- 找到一个显然在凸包上的点,比如 最左(或最下)的点 $p_0$,作为起点。
把 $p_0$ 作为当前点 $p$,然后重复:
在所有其它点中,找一个点 $q$,使得对任意其他点 $r$,
向量 $\overrightarrow{pq}$ 相比 $\overrightarrow{pr}$ 最“逆时针”(或者等价地,与当前基准方向极角最小)。
对于当前候选 $q$ 和另一个点 $r$,比较:$$ (r-p)\times(q-p) $$- 若 $>0$,则 $r$ 更逆时针,把 $q$ 换成 $r$;
- 否则保持 $q$。
- 当扫描完所有点后,$q$ 就是下一个凸包顶点。
- 把 $q$ 输出到凸包序列中,并令 $p\leftarrow q$ 继续。
- 直到新的 $q$ 又回到 $p_0$,停止。
也就是说,每确定一个凸包顶点,就需要对全部 $n$ 个点扫描一遍。
若凸包有 $h$ 个顶点,总工作量是 $O(nh)$。
复杂度结论:
- 当凸包点数 $h$ 很少(例如所有点都集中在内部),Jarvis 算法非常快;
- 当 $h$ 接近 $n$(比如点都在圆上),就变成 $O(n^2)$,反而比 Graham 慢。
4. 最近点对
- 预处理:按 $x$ 坐标把所有点排序一次。
分治:
- 把点集按中间的 $x$ 坐标分成左右两半 $L$ 和 $R$;
- 递归求出左半最近距离 $d_L$,右半最近距离 $d_R$;
- 令 $d=\min(d_L,d_R)$。
合并(关键步骤):
- 只需考虑“一点在左、一点在右”的最近点对;
- 可以证明:如果这样的最近点对距离小于 $d$,那么这两点必定都在垂直分界线两侧距离不超过 $d$ 的细长“带状区”里;
- 把这条带状区内的点按 $y$ 坐标排序,利用几何性质可以证明:
每个点只需要和它在 $y$ 方向上常数个后继比较距离即可(经典结论:最多检查 6~8 个邻居),
就能保证不会漏掉最近点对。
FFT
FFT实现多项式乘法过程:
输入:$A,B$ 的系数表示:
$$ \mathbf{a}=(a_0,\dots,a_{n-1}),\quad \mathbf{b}=(b_0,\dots,b_{n-1}) $$把每个多项式扩展到长度 $2n$ 的系数(后面补 $0$):
$$ (a_0,\dots,a_{n-1},0,\dots,0) $$- 把扩展后的系数转成在 $2n$ 个点上的点值:
这一步就是“多点求值(evaluation)”,如果用 FFT,只要 $\Theta(n\log n)$。 在点值形式下,逐点相乘:
$$ (x_k,,y_k) \cdot (x_k,,z_k) \Rightarrow (x_k,,y_k z_k) $$时间仅 $\Theta(n)$。
- 对乘完之后的 $2n$ 个点做插值(interpolation),还原为 $C(x)$ 的系数。
这一步用反向的 FFT(逆 DFT)也只要 $\Theta(n\log n)$。
综合下来,多项式乘法的时间是
1. 复数单位根(roots of unity)
设
称 $\omega_n$ 为“主 $n$ 次单位根”。所有的 $n$ 次单位根是
它们刚好在复平面的单位圆上均匀分布。欧拉公式是:
所以
这部分 PPT 讲了几个性质(只给结论):
有限群性质
$$ \omega_n^n = 1,\quad \omega_n^{j+k} = \omega_n^j \omega_n^k $$若 $n$ 为偶数,则
$$ \omega_n^{n/2} = -1 $$(在单位圆上转半圈就是 $-1$)
“等分引理”(Halving lemma)
当 $n$ 为偶数时,集合
$$ {\omega_n^{2k}\mid k=0,\dots,n/2-1} $$正好是所有 $(n/2)$ 次单位根。
“求和引理”(Summation lemma)
若 $k$ 不是 $n$ 的倍数,则
$$ \sum_{j=0}^{n-1} \omega_n^{kj} = 0 $$这个性质会用在证明逆 DFT 的公式正确。
2. DFT:在单位根处的多项式求值
现在选取特殊的 $n$ 个点:
对多项式
定义 离散傅里叶变换 DFT 为序列 $y_0,\dots,y_{n-1}$:
记作
这样,DFT 就是把“系数表示”变成“在单位根处的点值表示”。
如果直接按照定义算,每个 $y_k$ 都需要 $n$ 次乘加,总共 $n^2$,时间 $\Theta(n^2)$——太慢,这就是要用 FFT 加速的对象。
典型应用 4:离散信号转频域
把每个采样点 $s(t_i)$ 看成 $a_i$,形成序列
$$ \mathbf{a}=(a_0,\dots,a_{n-1}) $$做 DFT 得到
$$ \mathbf{y}=\operatorname{DFT}_n(\mathbf{a}) $$这就是频谱 $S(\omega)$ 的离散版本,告诉你信号里分别含有多少“不同频率”的成分。
3. FFT:用分治快速计算 DFT
FFT 使用了一个关键的分解式:
把多项式 $A(x)$ 的偶数项和奇数项分开:
那么
这一步只是重排。
接着要在所有 $x_k=\omega_n^k$ 上求值。注意:
利用“等分引理”,$x_k^2$ 其实就是 $n/2$ 次单位根。于是:
先对长度为 $n/2$ 的序列“偶数系数”做 DFT,得到
$$ y_k^{[0]}=A^{[0]}(\omega_{n/2}^k) $$再对“奇数系数”做 DFT,得到
$$ y_k^{[1]}=A^{[1]}(\omega_{n/2}^k) $$再利用
$$ A(\omega_n^k)=A^{[0]}(\omega_{n/2}^k)+\omega_n^kA^{[1]}(\omega_{n/2}^k) $$$$ A(\omega_n^{k+n/2})= A^{[0]}(\omega_{n/2}^k)-\omega_n^kA^{[1]}(\omega_{n/2}^k) $$把两个长度为 $n/2$ 的 DFT 合成一个长度为 $n$ 的 DFT。
这就是 FFT 的核心递推关系。伪代码结构大致是:
RECURSIVE-FFT(a):
n = len(a) // n 是 2 的幂
if n == 1: return a
a_even = (a[0], a[2], a[4], ...)
a_odd = (a[1], a[3], a[5], ...)
y_even = RECURSIVE-FFT(a_even)
y_odd = RECURSIVE-FFT(a_odd)
ω = e^{2πi/n}
ω_k = 1
for k = 0..n/2-1:
t = ω_k * y_odd[k]
y[k] = y_even[k] + t
y[k+n/2] = y_even[k] - t
ω_k = ω_k * ω
return y- 每一次递归,把问题大小减半($n\to n/2$),做两次 FFT;
- 合并阶段只需一趟循环,每层 $O(n)$;
- 总复杂度是 $\Theta(n\log n)$。
其中 $\omega_k$ 在合并时既被加上又被减去,这个乘数 $\omega_k$ 常称为 twiddle factor(旋转因子)。
典型应用 5:用 FFT 计算 DFT(示意版)
比如 $n=8$,输入 $(a_0,\dots,a_7)$,递归分解如下:
- 拆成偶数位置 $(a_0,a_2,a_4,a_6)$ 和奇数位置 $(a_1,a_3,a_5,a_7)$;
- 再对子序列长度 $4$ 继续拆成长度 $2$,直到长度 $1$;
- 自底向上,使用上述合并公式求出 $y_0,\dots,y_7$。
4. 逆 DFT(inverse DFT)与卷积定理
有了 DFT,自然要能“反过来”:给出 $y_k$ 还原 $a_j$。
逆 DFT 的公式是:
也可以写成矩阵形式,说“DFT 的矩阵 $V_n$ 的逆矩阵是 $V_n^{-1}$,其元素为 $\omega_n^{-kj}/n$”。从算法角度理解就够了:
如何用 FFT 实现逆 DFT?
- 把所有的 $\omega_n$ 换成 $\omega_n^{-1}$ 做一次 FFT;
- 然后把结果每一项都除以 $n$;
- 时间也是 $\Theta(n\log n)$。
卷积定理(Convolution theorem)告诉你:
设 $,\mathbf{a},\mathbf{b},$ 为长度 $n$ 的序列,把它们补零到长度 $2n$,则
这里 “$\cdot$” 是分量乘法,“$\odot$” 是卷积。
这就是“用 FFT 做卷积 / 多项式乘法”的理论基础,对应刚才的典型应用 3。
5. 蝶形运算(butterfly)
从递归 FFT 的合并步骤可以抽象出一个基本操作:
给定一对输入 $(u,v)$ 和一个“旋转因子” $\omega$,输出一对:
把这个图形画出来就是一个 “X” 形状,所以叫 蝶形运算。
典型应用 6:2 点 DFT 的蝶形
当 $n=2$ 时,DFT 就是:
这恰好是一次蝶形:$\omega=-1$,输出 $(a_0+a_1, a_0-a_1)$。
整个 FFT 可以看成是很多层、很多个蝶形堆叠起来。
6. 迭代 FFT 与 Bit-reversal
递归版容易理解,但在实际实现中会转成迭代版 FFT:
先对输入序列进行一次 bit-reversal 重排:
- 把下标用二进制写出来,
- 把二进制位反过来,
- 以这个新下标重新排列数据。
例如 $n=8$:
- 下标 $3$ 是二进制 $011$,翻转得到 $110$,即 $6$;
- 所以原来 $a_3$ 的位置上的数会被放到新数组的下标 $6$ 上。
- 然后从“块长 $2$ 的蝶形”开始,每一层把块长翻倍,直到块长 $n$;
- 在每一层,对每个块做对应的蝶形运算(用不同的旋转因子 $\omega$)。
迭代式的伪代码大致是:
ITERATIVE-FFT(a):
BIT-REVERSE-COPY(a, A) // 重排
for s = 1 .. log2 n:
m = 2^s
ω_m = e^{2πi/m}
for k = 0 .. n-1 step m:
ω = 1
for j = 0 .. m/2 - 1:
t = ω * A[k+j+m/2]
u = A[k+j]
A[k+j] = u + t
A[k+j+m/2] = u - t
ω = ω * ω_m
return A时间复杂度仍然是 $\Theta(n\log n)$。
典型应用 7:手算一个小例子
比如 $n=4$,输入 $(a_0,a_1,a_2,a_3)$:
对下标 $0,1,2,3$ 做 bit-reversal(2 位二进制):
- $00\to 00$(0)
- $01\to 10$(2)
- $10\to 01$(1)
- $11\to 11$(3)
排成 $(a_0,a_2,a_1,a_3)$;
- 第一层(块长 2):对 $(a_0,a_2)$、$(a_1,a_3)$ 做 2 点蝶形;
- 第二层(块长 4):再对上面结果做 4 点蝶形,得到最终 DFT 值。
字符串相关
- 给定文本串 $T[1..n]$ 和模式串 $P[1..m]$($m\le n$),字母表是有限集合 $\Sigma$,且 $P_i,T_i\in\Sigma$。
- 说“$P$ 在 $T$ 中以位移 $s$ 出现”,意思是:$0\le s\le n-m$ 且$$T[s+1..s+m] = P[1..m]\quad(\text{等价于 }T[s+j]=P[j],,1\le j\le m).$$
- 我们要找的是所有有效位移 valid shifts:所有满足上式的 $s$。
1.直接匹配
它把模式串当“模板”,从左到右枚举每个可能位移 $s=0..n-m$,每次检查:
最坏匹配时间:$\Theta((n-m+1)m)$(每个 $s$ 最多比对 $m$ 个字符)
2.Rabin–Karp
类似于哈希。把长度为 $m$ 的串看成一个 $d$ 进制数(或编码后的数),对模式串算一个值 $p(P)$,对每个对齐窗口 $T[s+1..s+m]$ 算 $p(T_{s+m})$:
- 若 $p(P)=p(T_{s+m})$ 则认为匹配;或更常用:
- 先比模:若 $(p(P)\bmod q)=(p(T_{s+m})\bmod q)$,再做一次“真匹配”检查 $P==T[s+1..s+m]$ 来排除冲突。
举例:字母 ${a,b,c,d}\mapsto{0,1,2,3}$,算出 $p(P)=99$(展示了按位权展开)。
3.有限自动机FA
一个有限自动机 $M$ 是五元组:$M=(Q,q_0,A,\Sigma,\delta),$ 读入字符时按 $\delta(q,a)$ 从状态 $q$ 跳到新状态。
后缀函数(suffix function)$\sigma$:
$\sigma(x)$ = “$x$ 的后缀中,最长的那段,恰好也是 $P$ 的前缀”的长度
转移函数: $\delta(q,a)=\sigma(P_q a).$
FINITE-AUTOMATON-MATCHER 就是:
- 初始化 $q=0$
- 逐个字符读 $T[i]$,令 $q\leftarrow\delta(q,T[i])$
- 若 $q==m$,说明刚读完一个匹配,输出位移 $i-m$。
4. KMP算法
对模式串 $P$,定义前缀函数:
\pi[q]=\max{k:;k<q\ \text{且}\ P_k\sqsupset P_q}.$$
这句话翻成中文就是:
在 $P[1..q]$ 的所有“真前缀”里,找一个最长的,它同时也是 $P[1..q]$ 的后缀;长度就是 $\pi[q]$。
四、排序与分治
五、动态规划
装配线调度 ALS
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
/**
* 阶段1:计算最短路径 (DP核心)
* 参数:
* n: 站点数 | a1,a2: 站处理时间 | t1,t2: 切换耗时
* e1,e2: 入口耗时 | x1,x2: 出口耗时
* l1,l2: [输出参数] 用于记录路径,需在外部resize(n)
* 返回值:pair<int, int> -> {最短总时间, 最后出来的线(1或2)}
*/
pair<int, int> getFastest(int n, const vector<int>& a1, const vector<int>& a2,
const vector<int>& t1, const vector<int>& t2,
int e1, int e2, int x1, int x2,
vector<int>& l1, vector<int>& l2) {
// dp数组:f1[i]表示到达线1第i站的最短时间
vector<int> f1(n), f2(n);
// 初始化第0站
f1[0] = e1 + a1[0];
f2[0] = e2 + a2[0];
// 状态转移 (从第1站开始遍历到n-1)
for (int j = 1; j < n; j++) {
// 计算线1:从线1直接来 vs 从线2切过来
if (f1[j-1] + a1[j] <= f2[j-1] + t2[j-1] + a1[j]) {
f1[j] = f1[j-1] + a1[j];
l1[j] = 1;
} else {
f1[j] = f2[j-1] + t2[j-1] + a1[j];
l1[j] = 2;
}
// 计算线2:从线2直接来 vs 从线1切过来
if (f2[j-1] + a2[j] <= f1[j-1] + t1[j-1] + a2[j]) {
f2[j] = f2[j-1] + a2[j];
l2[j] = 2;
} else {
f2[j] = f1[j-1] + t1[j-1] + a2[j];
l2[j] = 1;
}
}
// 计算加上离开时间后的总最优
if (f1[n-1] + x1 <= f2[n-1] + x2)
return {f1[n-1] + x1, 1}; // 最优线是1
else
return {f2[n-1] + x2, 2}; // 最优线是2
}
/**
* 阶段2:打印路径
* 参数:
* l1, l2: getFastest计算出的路径表
* lastL : 最后出来的线 (getFastest返回值的second)
* n : 站点数
*/
void printPath(int n, const vector<int>& l1, const vector<int>& l2, int lastL) {
int i = lastL;
cout << "Station " << n << ", Line " << i << endl; // 打印最后一站
// 倒序回溯:从 n-1 倒推到 1 (对应下标 n-1 到 1)
for (int j = n - 1; j >= 1; j--) {
// 如果当前在线1,查l1;在线2,查l2
i = (i == 1) ? l1[j] : l2[j];
cout << "Station " << j << ", Line " << i << endl;
}
}
int main() {
// 1. 准备输入数据
int n = 6;
int e1 = 2, e2 = 4;
int x1 = 3, x2 = 2;
// 处理时间 (大小为 n)
vector<int> a1 = {7, 9, 3, 4, 8, 4};
vector<int> a2 = {8, 5, 6, 4, 5, 7};
// 切换时间 (大小为 n-1)
vector<int> t1 = {2, 3, 1, 3, 4};
vector<int> t2 = {2, 1, 2, 2, 1};
// 2. 准备输出容器 (必须resize到n)
vector<int> l1(n), l2(n);
// 3. 调用核心算法
pair<int, int> res = getFastest(n, a1, a2, t1, t2, e1, e2, x1, x2, l1, l2);
// 4. 输出结果
cout << "Min Time: " << res.first << endl; // 输出最短时间
printPath(n, l1, l2, res.second); // 打印具体路线
return 0;
}
钢管切割问题
#include <vector>
#include <iostream>
#include <algorithm>
#include <climits> // 用于 INT_MIN
using namespace std;
// 1. 核心DP算法: 计算最大收益并记录方案
// 返回 pair: first是收益数组r, second是第一刀位置数组s
pair<vector<int>, vector<int>> extCutRod(const vector<int>& p, int n) {
vector<int> r(n + 1); // 收益表
vector<int> s(n + 1); // 方案表
r[0] = 0;
for (int j = 1; j <= n; ++j) {
int q = INT_MIN; // 初始化为负无穷
for (int i = 1; i <= j; ++i) { // i 代表尝试切下的这一段长度
// 状态转移: 当前一段价格 p[i] + 剩余部分最优解 r[j-i]
if (q < p[i] + r[j - i]) {
q = p[i] + r[j - i];
s[j] = i; // 记录造成最优解的第一刀长度
}
}
r[j] = q;
}
return {r, s};
}
// 2. 打印方案函数
// 逻辑: 不断输出当前s[n], 然后将n减去已输出的长度, 直到n为0
void printSol(const vector<int>& p, int n) {
// 调用DP函数获取表
pair<vector<int>, vector<int>> res = extCutRod(p, n);
vector<int> r = res.first;
vector<int> s = res.second;
cout << "最大收益: " << r[n] << endl;
cout << "切割方案: ";
while (n > 0) {
cout << s[n] << " "; // 打印这一刀的长度
n = n - s[n]; // 剩余长度
}
cout << endl;
}
int main() {
// 价格表:p[1]=1, p[2]=5, p[3]=8 ...
// p[0] 设为0占位,方便下标对应
vector<int> p = {0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30};
int n = 10; // 钢管总长
printSol(p, n);
return 0;
}
矩阵连乘 MCM
#include <iostream>
#include <vector>
#include <climits>
#include <algorithm>
using namespace std;
/*
* 功能:矩阵连乘最小运算次数 (MCM)
* 参数:
* p: 矩阵维度数组。共有 n = p.size()-1 个矩阵。
* 第 i 个矩阵 A_i 的维度为 p[i-1] x p[i]。
* 例如: A1(30x35), A2(35x15), A3(15x5) -> p = {30, 35, 15, 5}
* s: 记录分割点的二维数组 (引用传递,函数内会自动调整大小)
* 返回值:最小标量乘法次数
* 时间复杂度: O(n^3), 空间复杂度: O(n^2)
*/
long long mcm_solve(const vector<int>& p, vector<vector<int>>& s) {
int n = p.size() - 1;
// m[i][j] 存储 Ai..Aj 的最小代价
// 为了防止溢出,使用 long long
vector<vector<long long>> m(n + 1, vector<long long>(n + 1, 0));
s.assign(n + 1, vector<int>(n + 1, 0));
// l 是链的长度,从 2 开始到 n
for (int l = 2; l <= n; l++) {
for (int i = 1; i <= n - l + 1; i++) {
int j = i + l - 1;
m[i][j] = LLONG_MAX; // 初始化为无穷大
// k 是分割点,将 Ai..Aj 分割为 Ai..Ak 和 Ak+1..Aj
for (int k = i; k < j; k++) {
// 代价 = 左边代价 + 右边代价 + 合并代价
long long q = m[i][k] + m[k + 1][j] + (long long)p[i - 1] * p[k] * p[j];
if (q < m[i][j]) {
m[i][j] = q;
s[i][j] = k; // 记录最优分割点
}
}
}
}
return m[1][n];
}
/*
* 功能:根据 s 表打印最优括号方案
* 参数:s (由 mcm_solve 生成), i (起点), j (终点)
* 调用方式: print_parens(s, 1, n); cout << endl;
*/
void print_parens(const vector<vector<int>>& s, int i, int j) {
if (i == j) {
cout << "A" << i;
} else {
cout << "(";
print_parens(s, i, s[i][j]);
print_parens(s, s[i][j] + 1, j);
cout << ")";
}
}
// --------------------------------------------------------
// 使用案例 (考试时只需抄写上面的函数,下面是主函数示例)
int main() {
// 示例:A1(30x35), A2(35x15), A3(15x5), A4(5x10), A5(10x20), A6(20x25)
vector<int> p = {30, 35, 15, 5, 10, 20, 25};
vector<vector<int>> s;
long long cost = mcm_solve(p, s);
cout << "Minimum Cost: " << cost << endl; // 应输出 15125
cout << "Optimal Parenthesization: ";
print_parens(s, 1, p.size() - 1); // 应输出 ((A1(A2A3))((A4A5)A6))
cout << endl;
return 0;
}最优二叉搜索树 OBST
#include <iostream>
#include <cfloat> // 用于 DBL_MAX
using namespace std;
const int MAX = 205; // 根据题目数据范围调整,防止越界
double e[MAX][MAX]; // e[i][j]: 搜索最优期望代价
double w[MAX][MAX]; // w[i][j]: 概率总权重
int r[MAX][MAX]; // r[i][j]: 区间[i,j]的最优根节点下标
/**
* OBST 算法 (Knuth 优化版 O(n^2))
* @param n 关键字个数
* @param p 成功概率数组,下标从 1 到 n
* @param q 失败概率数组,下标从 0 到 n
* 说明:计算完成后,e[1][n] 为最小代价,r[1][n] 为整棵树的根
*/
void obst(int n, double p[], double q[]) {
// 1. 初始化空区间 (对应伪代码第一个循环)
for (int i = 1; i <= n + 1; i++) {
e[i][i - 1] = q[i - 1];
w[i][i - 1] = q[i - 1];
}
// 2. l 表示区间长度 (对应伪代码第二个循环)
for (int l = 1; l <= n; l++) {
// i 为区间起点
for (int i = 1; i <= n - l + 1; i++) {
int j = i + l - 1; // j 为区间终点
e[i][j] = DBL_MAX; // 初始化无穷大
// O(1) 更新权重 w
w[i][j] = w[i][j - 1] + p[j] + q[j];
// Knuth 优化核心:缩小根 k 的枚举范围
// 原始范围: [i, j]
// 优化范围: [r[i][j-1], r[i+1][j]]
// 边界处理: 当 l=1 时,范围就是 [i, i]
int start = (l == 1) ? i : r[i][j - 1];
int end = (l == 1) ? j : r[i + 1][j];
// 尝试可能的根 k
for (int k = start; k <= end; k++) {
// 代价计算公式: 左子树代价 + 右子树代价 + 当前权重
double t = e[i][k - 1] + e[k + 1][j] + w[i][j];
if (t < e[i][j]) {
e[i][j] = t;
r[i][j] = k; // 记录最优根
}
}
}
}
}
/**
* 递归打印 OBST 结构
* @param i 当前子树的左边界
* @param j 当前子树的右边界
* @param p 父节点编号 (parent),初始调用传 0
* @param type 类型:0=根节点, 1=左孩子, 2=右孩子
* 注意:依赖全局变量 r[MAX][MAX]
*/
void print_tree(int i, int j, int p, int type) {
// 1. 递归终止条件:如果是空树(遇到虚拟键 d)
if (i > j) {
// 如果题目要求输出虚拟键 d_k,可以在这里加上:
// int d_index = j; // 或者是 i-1
// if (type==1) cout << "d" << d_index << " is Left Child of k" << p << endl;
// else cout << "d" << d_index << " is Right Child of k" << p << endl;
return;
}
// 2. 获取当前子树的根
int k = r[i][j];
// 3. 打印当前节点信息
if (type == 0) {
cout << "k" << k << " is Root" << endl;
} else if (type == 1) {
cout << "k" << k << " is Left Child of k" << p << endl;
} else {
cout << "k" << k << " is Right Child of k" << p << endl;
}
// 4. 递归处理左右子树
print_tree(i, k - 1, k, 1); // 左子树 (type=1)
print_tree(k + 1, j, k, 2); // 右子树 (type=2)
}
int main() {
// 示例数据:n=5
// p 从下标 1 开始,p[0] 占位
// q 从下标 0 开始
int n = 5;
double p[] = {0.0, 0.15, 0.10, 0.05, 0.10, 0.20};
double q[] = {0.05, 0.10, 0.05, 0.05, 0.05, 0.10};
// 调用板子
obst(n, p, q);
// 输出结果
cout << "Minimum Cost: " << e[1][n] << endl;
cout << "Root of Tree: " << r[1][n] << endl;
cout << "The Optimal Binary Search Tree Structure:" << endl;
// 初始调用:范围 1 到 n,父节点设为 0(无),类型设为 0(根)
print_tree(1, n, 0, 0);
return 0;
}最长上升子序列
#include<iostream>
using namespace std;
int main()
{
int n;
cin >> n;
int a[n],dp[n];
for(int i = 0;i<n;i++)
{
cin >> a[i];
dp[i] = 1;//自身一定是一个长度的序列
}
for(int i = 1;i<n;i++)
{
for(int j = 0;j<i;j++)
{
if(a[i] > a[j])//因为是上升,所以需要只有比前面的值大才可能形成最长上升子序列
{
if(dp[i] < dp[j]+1) dp[i] = dp[j] + 1;//记录i处最长的上升序列长度
//即前面的序列长度最大长度+1即是i处的最大长度
}
}
}
int max = dp[0];//不一定最后一个是最长的,因此需要获取最大值
for(int i = 1;i<n;i++)
{
if(max < dp[i]) max = dp[i];
}
cout << max << '\n';
return 0;
}最长公共子序列
#include <iostream>
#include <vector>
#include <string>
#include <algorithm> // 必须包含: max, reverse
using namespace std;
/*
* [函数1: 核心DP计算]
* 功能: 生成LCS的DP表格
* 参数: a, b (待比较的两个字符串)
* 返回: 二维vector表,dp[n][m]即为LCS长度
* 复杂度: 时间 O(NM), 空间 O(NM)
*/
vector<vector<int>> get_dp(const string& a, const string& b) {
int n = a.size();
int m = b.size();
// 初始化 (n+1)*(m+1) 的二维数组,全为0
vector<vector<int>> dp(n + 1, vector<int>(m + 1, 0));
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
if (a[i - 1] == b[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp;
}
/*
* [函数2: 恢复LCS字符串]
* 功能: 调用函数1获取DP表,倒推还原出最长公共子序列
* 参数: a, b (必须与传给函数1的一致)
* 返回: LCS 具体字符串
*/
string get_lcs(const string& a, const string& b) {
// 1. 调用第一个函数,获取“地图” (DP表)
vector<vector<int>> dp = get_dp(a, b);
// 2. 准备回溯
string res;
int i = a.size();
int j = b.size();
// 3. 根据“地图”倒着走
while (i > 0 && j > 0) {
if (a[i - 1] == b[j - 1]) {
// 只有字符相等时,才来自于左上角,且该字符属于LCS
res += a[i - 1];
i--; j--;
} else {
// 字符不等,来源于数值较大的方向(左或上)
if (dp[i - 1][j] > dp[i][j - 1]) i--;
else j--;
}
}
// 4. 倒推的结果是反的,需要翻转回来
reverse(res.begin(), res.end());
return res;
}
// =================== 考试使用案例 ===================
int main() {
// 优化输入输出效率 (考试必备)
ios::sync_with_stdio(false);
cin.tie(0);
string s1 = "ABCBDAB";
string s2 = "BDCABA";
// 场景 A: 只需要长度
// 直接调用第一个函数,取右下角的值
vector<vector<int>> table = get_dp(s1, s2);
cout << "LCS Length: " << table[s1.size()][s2.size()] << endl;
// 场景 B: 需要具体字符串
// 调用第二个函数 (它内部会自动调用第一个)
string lcs_str = get_lcs(s1, s2);
cout << "LCS String: " << lcs_str << endl;
return 0;
}
最长公共子串
子串:需要连续的,与子序列不同
#include <iostream>
#include <string>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;
// 全局变量方便抄写,防止栈溢出
// MAXN 根据题目数据范围修改,例如 1005 或 5005
const int MAXN = 1005;
int f[MAXN][MAXN]; // DP数组
int mx = 0; // 最长公共子串的长度
int endPos = 0; // 最长子串在字符串 a 中的结束位置(1-based)
/*
* 函数名: getLCS
* 功能: 计算两个字符串的最长公共子串长度及位置
* 参数: string a, string b - 需要比较的两个字符串
* 注意: f[i][j] 表示以 a[i-1] 和 b[j-1] 结尾的最长公共子串长度
*/
void getLCS(string a, string b) {
int n = a.size();
int m = b.size();
// 初始化 (如果是多组数据测试,必须加 memset)
mx = 0;
memset(f, 0, sizeof(f));
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (a[i - 1] == b[j - 1]) {
f[i][j] = f[i - 1][j - 1] + 1;
// 更新最大值和结束位置
if (f[i][j] > mx) {
mx = f[i][j];
endPos = i; // 记录在 a 中的位置(1-based)
}
} else {
f[i][j] = 0; // 子串必须连续,不匹配则断开
}
}
}
}
/*
* 函数名: printLCS
* 功能: 打印最长公共子串的内容
* 参数: string a - 原始字符串 a (用于提取子串)
* 说明: 必须先调用 getLCS 计算出 mx 和 endPos
*/
void printLCS(string a) {
if (mx == 0) {
cout << "No Common Substring" << endl;
return;
}
// substr(起始下标, 长度)
// endPos 是 1-based,转回 0-based 需要 -1,再减去长度 mx 还没减完,
// 起始位置 = (endPos - 1) - mx + 1 = endPos - mx
cout << a.substr(endPos - mx, mx) << endl;
}
// --- 使用案例 ---
/*
int main() {
string s1 = "acbcbcef";
string s2 = "abcbced";
getLCS(s1, s2);
cout << "最大长度: " << mx << endl; // 输出: 5
cout << "公共子串: ";
printLCS(s1); // 输出: bcbce
return 0;
}
*/01背包问题
给定背包总体积,给N个物品,每个物品有一个体积和重量,只能用一次或不用,问最大重量是多少?
定义函数f(i,j)代表:仅包含前i个物品且总体积小于等于j的背包的最大价值是多少,故最终需要的结果是f(N,V)。
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main(){
cin >> n >> m;
for(int i=1; i <= n; i++) cin >> v[i] >> w[i];
for(int i=1; i <= n; i++){
for(int j = 1; j <= m; j++){
f[i][j] = f[i-1][j];
if(j >= v[i]) f[i][j] = max(f[i][j], f[i-1][j-v[i]] + w[i]);
}
// 一维数组
//for(int j = m; j >= 1; j--){
//if(j >= v[i]) f[j] = max(f[j], f[j-v[i]] + w[i]);
//}
}
cout << f[n][m] << endl;
}完全背包问题
完全背包的区别是每个物品可以选0-无数次,同样求最大总重量。
思路: 此时DP数组的含义不变。在每次选择f(i,j)时,同样也变成了k+1种选择(选择0,1,2,…,k个第i个元素,k由循环判断当前的j能否大于或等于k个i的价值,即k*wi <= j),循环判断出其中的最大值,就可以算出新的f[i,j]。
因为循环的嵌套是从i: 1-N, j: i-V计算的,所以在计算f[i,j]时,f[i, j-v]必然被算过(v代表i的体积,w代表i的重量)。f[i,j]与f[i, j-v]之间存在如下的联系:
那么可以看出两者的关系为
则此时减少了一层循环,提高运行效率。
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];
int main(){
cin >> n >> m;
for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
for(int i = 1; i <= n; i ++){
for(int j = 0; j <= m; j++){
// 改为一维
// f[i][j] = f[i - 1][j];
// if (j >= v[i]) f[i][j] = max(f[i][j], f[i][j-v[i]] + w[i]);
if (j >= v[i]) f[j] = max(f[j], f[j-v[i]] + w[i]);
}
}
cout << f[n][m] << endl;
return 0;
}多重背包问题
这个算法是 多重背包问题的二进制拆分优化,它将第 $i$ 种物品的 $s$ 个拆分成 $1, 2, 4, \dots, 2^k, \text{remainder}$ 个捆绑包,然后转化为 0/1 背包问题求解。

/*
多重背包问题 - 二进制拆分优化
输入: n(物品种类), m(背包容量)
接下来n行: a(体积), b(价值), s(数量)
原理: 将多重背包转化为 0/1 背包
时间复杂度: O(m * Σlog(s_i))
*/
#include <iostream>
#include <algorithm>
using namespace std;
// 数据范围预估:
// 假设 N=1000, log(S)≈12 (S=2000),
// 拆分后的物品总数约为 12000 左右,这里开大一点防止越界
const int MAX_N = 25000;
const int MAX_M = 2010; // 背包容量
int n, m;
int v[MAX_N]; // 存储拆分后的体积 (Volume)
int w[MAX_N]; // 存储拆分后的价值 (Worth/Weight)
int f[MAX_M]; // DP数组
int main()
{
cin >> n >> m;
int cnt = 0; // 记录拆分后的新物品总数
for (int i = 1; i <= n; i ++ )
{
int a, b, s;
cin >> a >> b >> s; // a:单件体积, b:单件价值, s:数量
int k = 1;
while (k <= s)
{
cnt ++ ;
v[cnt] = a * k;
w[cnt] = b * k;
s -= k;
k *= 2;
}
if (s > 0)
{
cnt ++ ;
v[cnt] = a * s;
w[cnt] = b * s;
}
}
n = cnt; // 更新物品总数为拆分后的数量
// 下面是标准的 0/1 背包模板
for (int i = 1; i <= n; i ++ )
for (int j = m; j >= v[i]; j -- )
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << endl;
return 0;
}
分组背包问题
物品被分成若干组,每组中的物品只能选择一个。
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
const int MAX = 1005;
struct {
int cnt;
ll ID[MAX];
} group[MAX]; //用一个结构体来存储每一组的物品编号
ll dp[MAX]; // 最大价值
ll val[MAX]; // 每个物品的价值
ll weight[MAX]; // 每个物品的重量
ll group_bag(int cap, int max_group);
int main() {
int n, W;
cin >> W >> n; // n表示物品数量,W表示背包容量
int a, b, k, max_group = 0;
for (int i = 1; i <= n; i++) {
cin >> a >> b >> k; // a重量 b价值 k物品所在的组号
weight[i] = a;
val[i] = b;
group[k].ID[group[k].cnt++] = i;
max_group = max(max_group, k);
}
cout << group_bag(W, max_group);
return 0;
}
ll group_bag(int W, int max_group) {
for (int i = 0; i <= max_group; i++) // 第一层循环,遍历所有组
for (ll j = W; j >= 0; j--) // 第二层循环,从背包容量W到0倒序遍历
for (int k = 0; k < group[i].cnt; k++) // 第三层循环,遍历当前组内的所有物品
if (j >= weight[group[i].ID[k]]) // 如果当前物品可以放入背包
// 更新dp数组,选择放入或不放入当前物品,取最大值
dp[j] = max(dp[j],dp[j - weight[group[i].ID[k]]] + val[group[i].ID[k]]);
return dp[W];
}石子合并(区间DP)
区间DP的核心是:大区间由小区间合并而来。
循环顺序:先枚举长度 len,再枚举左端点 i,最后枚举分割点 k。
/*
* [区间 DP - 通用思考骨架]
* 适用:石子合并、括号匹配、能量项链、回文子串等。
* 核心思想:从小区间向大区间递推。
* 状态:dp[i][j] 表示区间 [i, j] 的最优解。
* 复杂度:O(N^3)
*
* 参数说明:
* n: 元素个数
* dp[N][N]: 状态数组,注意初始化 (求Min初始化为INF, 求Max初始化为0)
* w(i, j): 合并区间 [i, j] 产生的额外代价 (如前缀和计算)
*/
#include <algorithm>
#include <cstring>
using namespace std;
const int INF = 0x3f3f3f3f;
int dp[505][505]; // 根据题目数据范围调整
int s[505]; // 前缀和数组,用于快速计算区间和
void solve_interval(int n, int a[]) {
// 1. 初始化
// 如果求最大值,memset(dp, 0); 如果求最小值,memset(dp, 0x3f);
// 基础状态:长度为1的区间代价通常为0
for (int i = 1; i <= n; i++) {
dp[i][i] = 0;
s[i] = s[i-1] + a[i]; // 预处理前缀和
}
// 2. 循环主体 (必须背诵这个顺序)
// 第一层:枚举区间长度 (从2开始,直到n)
for (int len = 2; len <= n; len++) {
// 第二层:枚举左端点 i
for (int i = 1; i + len - 1 <= n; i++) {
int j = i + len - 1; // 计算右端点 j
dp[i][j] = INF; // 初始化当前大区间,准备更新
// 第三层:枚举分割点 k (区间 [i, j] 被分成 [i, k] 和 [k+1, j])
// 注意 k 的范围:[i, j-1]
for (int k = i; k < j; k++) {
// 状态转移方程:左边最优 + 右边最优 + 合并代价
// cost = s[j] - s[i-1]; // 例如石子合并的代价是区间和
int cost = s[j] - s[i-1];
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k+1][j] + cost);
}
}
}
// 答案通常是 dp[1][n]
}
六、贪心算法
最多活动数(区间调度)
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
// 定义活动结构体:s为开始时间,f为结束时间
struct Act {
int s, f;
};
/**
* 算法板子:区间调度/活动选择问题
*
* @param a 活动列表 (vector<Act>)
* @return int 最多能参加的活动数量
*
* 使用说明:
* 1. 确保输入的区间格式为 [s, f)。即 f 是结束时刻,不包含 f 本身。
* (若题目定义包含结束时刻,即[s, f],则判定条件改为 x.s > last)
* 2. 核心逻辑:按结束时间 f 升序排序,遍历选择不重叠的活动。
* 3. 复杂度:时间 O(N log N) (排序耗时),空间 O(1) (不含输入存储)。
*/
int maxActs(vector<Act>& a) {
if (a.empty()) return 0;
// 1. 按结束时间从小到大排序
// lambda表达式写法,方便抄写。如果f相同,s的顺序不影响最大数量。
sort(a.begin(), a.end(), [](const Act& x, const Act& y) {
return x.f < y.f;
});
int cnt = 0; // 计数器
int last = -2e9; // 记录上一个选中活动的结束时间,初始化为负无穷
// 2. 遍历并选择
for (auto& x : a) {
// 如果当前活动开始时间 >= 上个活动结束时间,说明相容
if (x.s >= last) {
cnt++;
last = x.f; // 更新结束时间
}
}
return cnt;
}
// ================= 使用案例 =================
int main() {
// 示例输入:5个活动
// [1, 4), [3, 5), [0, 6), [5, 7), [3, 9), [5, 9), [6, 10), [8, 11), [8, 12), [2, 14), [12, 16)
// 这里简单构造几个数据演示
vector<Act> acts = {
{1, 4}, {3, 5}, {0, 6}, {5, 7},
{3, 9}, {5, 9}, {6, 10}, {8, 11},
{8, 12}, {2, 14}, {12, 16}
};
int result = maxActs(acts);
cout << "最大兼容活动数: " << result << endl;
// 对于上述标准数据(算法导论例题),正确输出应为 4
// 选出的活动可能是: [1,4), [5,7), [8,11), [12,16)
return 0;
}Huffman编码
AI版
#include <bits/stdc++.h>
using namespace std;
/*
* 参数说明:
* cnt: map<char, int> 存储字符及其出现频率 (例如 {'a':5, 'b':9})
* 返回值:
* map<char, string> 存储字符对应的哈夫曼编码 (例如 {'a':"110", 'b':"10"})
* 复杂度:
* 时间 O(N log N), 空间 O(N)
*/
// 树节点结构体
struct Node {
char c; // 字符
int w; // 权值(频率)
Node *l, *r; // 左右子树
Node(char v, int f) : c(v), w(f), l(0), r(0) {}
};
// 优先队列比较器 (小根堆)
struct Cmp {
bool operator()(Node* a, Node* b) {
return a->w > b->w; // 频率小的优先级高
}
};
// DFS 遍历生成编码
void dfs(Node* u, string code, map<char, string> &res) {
if (!u) return;
// 如果是叶子节点,记录编码
if (!u->l && !u->r) {
res[u->c] = code;
return;
}
dfs(u->l, code + "0", res); // 左边为0
dfs(u->r, code + "1", res); // 右边为1
}
// 主函数: 生成哈夫曼编码
map<char, string> huffman(map<char, int> &cnt) {
priority_queue<Node*, vector<Node*>, Cmp> q;
// 1. 初始化: 所有字符入队
for (auto &p : cnt) q.push(new Node(p.first, p.second));
// 2. 构建哈夫曼树: 合并 n-1 次
while (q.size() > 1) {
Node *x = q.top(); q.pop(); // 取最小
Node *y = q.top(); q.pop(); // 取次小
// 新节点权值为两者之和,内部节点字符通常设为空或特殊值
Node *z = new Node('\0', x->w + y->w);
z->l = x; z->r = y;
q.push(z);
}
// 3. 生成编码表
map<char, string> codes;
if (!q.empty()) dfs(q.top(), "", codes);
return codes;
}
int main() {
// 示例输入: "abacaba" 或直接给出频率
// 频率: a:4, b:2, c:1
map<char, int> freq;
freq['a'] = 4;
freq['b'] = 2;
freq['c'] = 1;
freq['d'] = 1; // 随便加点数据
// 调用板子
map<char, string> huffmanCodes = huffman(freq);
// 输出结果
cout << "Char | Code" << endl;
for (auto &p : huffmanCodes) {
cout << " " << p.first << " | " << p.second << endl;
}
// 模拟计算 WPL (带权路径长度)
int wpl = 0;
for (auto &p : huffmanCodes) {
wpl += freq[p.first] * p.second.length();
}
cout << "WPL: " << wpl << endl;
return 0;
}仅计算长度:
#include <bits/stdc++.h>
using namespace std;
int a[300];
long long n = 0;
struct node{
struct node *left;
struct node *right;
long long sum;
};
struct compare {
bool operator()(node* a, node* b) const {
return a->sum > b->sum;
}
};
priority_queue<node*, vector<node*>, compare> que;
int main(){
char x; n = 0;
while(scanf("%c", &x)!=EOF){
if (('A' <= x && x <= 'Z') || ('a' <= x && x <= 'z')){a[(int)x]++;n++;}
}
for(int i='A'; i<='Z';i++){
if(a[i]==0) continue;
struct node* aa = (struct node*)malloc(sizeof(struct node));
aa->left = NULL; aa->right = NULL; aa->sum = a[i];
que.push(aa);
}
for(int i='a'; i<='z';i++){
if(a[i]==0) continue;
struct node* aa = (struct node*)malloc(sizeof(struct node));
aa->left = NULL; aa->right = NULL; aa->sum = a[i];
que.push(aa);
}
if (que.size() == 1) {
printf("%lld\n", n);
return 0;
}
long long ans = 0;
while(que.size()>1){
struct node* newnew = (struct node*)malloc(sizeof(struct node));
long long all = 0;
struct node* na = que.top(); que.pop();
all += na->sum;
newnew->left = na;
na = que.top(); que.pop();
all += na->sum;
newnew->right = na;
newnew->sum = all;
ans += all;
que.push(newnew);
}
cout << ans;
return 0;
}七、图算法
链式前向星
/*
* 参数说明:
* V_MAX: 最大点数
* E_MAX: 最大边数 (注意:如果是无向图,E_MAX 需要开边数的2倍)
* head[]: 存储每个点头部边的索引,初始化为-1
* Edge结构体: to(终点), w(权值), next(下一条同起点的边)
*/
const int N = 10005; // 最大点数 (根据题目改)
const int M = 20005; // 最大边数 (无向图记得 * 2)
const int INF = 0x3f3f3f3f; // 无穷大 (约10亿,memset可用)
struct Edge{
int to, w, next; //终点,权值,前驱
} e[E_MAX];
int cnt_E = 0;
int head[V_MAX]; //需要先初始化为-1
void initList(int n){
memset(head, -1, sizeof(head));
}
// 加边函数 (无向图需要调用两遍)
void addEdge(int x, int y, int w) {
e[cnt_E].to = y;
e[cnt_E].w = w;
e[cnt_E].next = head[x];
head[x] = cnt_E++;
}
// 【核心】遍历模版:访问从 u 点出发的所有边
// 考试时直接套用这个 for 循环
void traverse(int u) {
// i 代表边的索引
for (int i = head[u]; i != -1; i = e[i].next) {
int v = e[i].to; // 这条边的终点
int w = e[i].w; // 这条边的权值
// 在这里进行你的操作,例如:
// if (!visited[v]) dfs(v);
// if (dist[v] > dist[u] + w) ...
}
}
用不了的情况:Floyd-Warshall 算法(多源最短路)
// 仅当 N <= 500 时使用
int g[505][505];
// 初始化:自己到自己是0,其他是无穷大
// memset(g, 0x3f, sizeof(g));
// for(int i=1; i<=n; i++) g[i][i] = 0;
// 加边 u -> v 权值 w
// g[u][v] = min(g[u][v], w); // 防止重边,取最小
问题:如果有操作问你:“点 A 和 点 B 之间有直接相连的边吗?”
链式前向星:需要遍历 head[A] 的所有边,看有没有指向 B 的。复杂度是 $O(\text{degree of A})$。
邻接矩阵:直接看 if (g[A][B] != INF)。复杂度是 $O(1)$。
DFS 深度优先搜索
适用场景: 连通性判断、找环、树的遍历、求子树大小。
/* for 链式前向星
* DFS板子
* vis[]: 标记数组,防止重复访问
* u: 当前节点
*/
bool vis[N];
void dfs(int u) {
vis[u] = true; // 标记当前点已访问
// 遍历 u 的所有出边
for (int i = head[u]; i != -1; i = e[i].next) {
int v = e[i].to;
int w = e[i].w; // 如果需要权值
if (!vis[v]) {
// 在这里可以处理父子关系,如: parent[v] = u;
dfs(v);
}
}
}bool is_visit[maxn];
void dfs_visit(int v) { // 深度优先搜索
is_visit[v] = 1;
// 此处添加访问逻辑
for(int edge_inx = h[v]; ~edge_inx; edge_inx = ne[edge_inx]) {
if(!is_visit[e[edge_inx]]) {
dfs_visit(e[edge_inx]);
}
}
// 访问退出时间戳
}
void dfs(int n) {
memset(is_visit, 0, sizeof(bool) * (n + 2));
for(int i = 1; i <= n; i++) {
if(!is_visit[i]) {
dfs_visit(i);
}
}
}BFS 广度优先搜索
适用场景: 无权图的最短路径、层序遍历、拓扑排序。
/* for 链式前向星
* BFS板子 (求无权图最短路)
* s: 起点
* dist[]: 存储起点到各点的距离,兼顾了 visited 数组的功能
*/
int dist[N]; // 距离数组
void bfs(int s) {
// 1. 初始化距离为 -1 (表示未访问)
memset(dist, -1, sizeof(dist));
queue<int> q;
// 2. 起点入队
dist[s] = 0;
q.push(s);
while (!q.empty()) {
int u = q.front(); q.pop();
// 3. 遍历邻居
for (int i = head[u]; i != -1; i = e[i].next) {
int v = e[i].to;
// 如果 v 未被访问过
if (dist[v] == -1) {
dist[v] = dist[u] + 1; // 距离 +1
q.push(v);
}
}
}
}bool is_visit[maxn];
void bfs_visit(int v) { // 广度优先搜索,使用栈存储
is_visit[v] = 1;
queue<int> q;
q.push(v);
while (!q.empty()) {
v = q.front();
q.pop();
for(int edge_inx = h[v]; ~edge_inx; edge_inx = ne[edge_inx]) {
if(!is_visit[e[edge_inx]]) {
// 访问逻辑
bfs_visit(e[edge_inx]);
q.push(e[edge_inx]);
}
}
}
}
void bfs(int n) {
memset(is_visit, 0, sizeof(bool) * (n + 2));
for(int i = 1; i <= n; i++) {
if(!is_visit[i]) {
bfs_visit(i);
}
}
}拓扑排序
在一个有向无环图(DAG)中,找到一种线性顺序,把所有顶点排成列,使得:
- 对每条边 $(u,v)$,$u$ 都出现在 $v$ 前面。
伪代码简化版:
- 对图做 BFS,记录所有 $f[v]$。
- 把所有顶点按 $f[v]$ 从大到小排序,得到序列 $L$。
- 输出 $L$ 即拓扑序。
/*
* 拓扑排序参数说明:
* n: 点的总数
* deg[]: 入度数组 (关键!读入边时记得 deg[v]++)
* topo[]: 存储最终的拓扑序列
* 返回值: true 表示成功,false 表示图中有环
*/
int deg[N]; // 入度数组
int topo[N], t_cnt; // 结果数组 和 计数器
bool toposort(int n) {
t_cnt = 0;
queue<int> q;
// 如果题目要求字典序最小,把上一行换成:
// priority_queue<int, vector<int>, greater<int>> q;
// 1. 将所有初始入度为 0 的点入队
for (int i = 1; i <= n; i++) {
if (deg[i] == 0) q.push(i);
}
while (!q.empty()) {
int u = q.front(); q.pop(); // 取出队头
// 如果是优先队列,用 int u = q.top(); q.pop();
topo[++t_cnt] = u; // 加入结果序列
// 2. 遍历 u 的所有出边,模拟“删边”操作
for (int i = head[u]; i != -1; i = e[i].next) {
int v = e[i].to;
deg[v]--; // v 的入度减 1
if (deg[v] == 0) {
q.push(v); // 如果入度变为 0,则入队
}
}
}
// 3. 判断是否所有点都进入了序列
// 如果少于 n,说明有环,剩余的点互为前驱,无法入队
return t_cnt == n;
}
int main() {
int n, m;
cin >> n >> m;
// 0. 初始化
memset(head, -1, sizeof(head));
cnt_E = 0;
memset(deg, 0, sizeof(deg)); // 清空入度
// 1. 读入边
for (int i = 0; i < m; i++) {
int u, v;
cin >> u >> v;
addEdge(u, v, 0); // 有向图,权值通常不需要,填0
deg[v]++; // 【关键】统计入度!这一步千万别漏!
}
// 2. 调用拓扑排序
if (toposort(n)) {
// 输出结果
for (int i = 1; i <= n; i++) {
cout << topo[i] << " ";
}
} else {
cout << "有环,无法排序"; // 比如输出 -1
}
return 0;
}
最小生成树
Kruskal算法
// =================================================
// 算法 1: Kruskal
// 适用:稀疏图 | 复杂度:O(E log E)
// 核心依赖:并查集 + 边排序
// =================================================
/*
逻辑核心(方便背诵):
1. 转换:将链式前向星的边转存为 {u, v, w} 数组(因为Kruskal需要遍历所有边并排序)。
2. 排序:按权值 w 从小到大排序。
3. 循环:遍历排序后的边,若 find(u) != find(v)(不连通),则合并 unite(u, v),累加权值,边数+1。
4. 判断:若选中边数 == n-1,成功;否则图不连通。
*/
// 为了Kruskal专门定义的简单结构体,方便排序
struct KEdge {
int u, v, w;
bool operator<(const KEdge &other) const {
return w < other.w;
}
};
int fa[N]; // 并查集数组
// 并查集查找 (路径压缩)
int find(int x) {
return x == fa[x] ? x : fa[x] = find(fa[x]);
}
/*
* 函数名: kruskal
* 参数: n (点数)
* 返回: 最小生成树权值和 (若不连通返回 -1)
* 注意: 调用前需正常建图 addEdge
*/
int kruskal(int n) {
// 1. 初始化并查集
for (int i = 1; i <= n; i++) fa[i] = i;
// 2. 将链式前向星数据提取到临时数组 (方便排序)
// 考试技巧:如果题目直接给边列表,可跳过链式前向星直接读入到 kEdges
vector<KEdge> kEdges;
for (int u = 1; u <= n; u++) {
for (int i = head[u]; i != -1; i = e[i].next) {
int v = e[i].to;
// 链式前向星无向图存了两遍,为了不重复算,只取 u < v 的边
if (u < v) {
kEdges.push_back({u, v, e[i].w});
}
}
}
// 3. 排序
sort(kEdges.begin(), kEdges.end());
// 4. 贪心选边
int res = 0, cnt = 0;
for (auto &edge : kEdges) {
int rootU = find(edge.u);
int rootV = find(edge.v);
if (rootU != rootV) {
fa[rootU] = rootV; // 合并
res += edge.w;
cnt++;
}
}
// 5. 判断连通性 (n个点需要 n-1 条边)
if (cnt < n - 1) return -1;
return res;
}非链式前向星:
#include <iostream>
#include <algorithm> // 必须包含,用于 sort
using namespace std;
// ================== 参数配置 ==================
const int N = 10005; // 最大点数
const int M = 200005; // 最大边数 (注意:Kruskal存边是线性的,无向图存一次即可,不需要*2)
// ================== 数据结构 ==================
struct Edge {
int u, v, w;
// 重载 < 运算符,sort时自动按权值排序
bool operator<(const Edge &t) const {
return w < t.w;
}
} edges[M]; // 边集数组
int fa[N]; // 并查集数组
// ================== 核心函数 ==================
// 并查集查找 (含路径压缩)
int find(int x) {
return x == fa[x] ? x : fa[x] = find(fa[x]);
}
/*
* 函数名: kruskal
* 参数: n (点数), m (边数)
* 返回: 最小生成树权值和 (若不连通返回 -1)
* 注意: 请确保 edges[1...m] 已经读入了数据
*/
int kruskal(int n, int m) {
// 1. 初始化并查集
for (int i = 1; i <= n; i++) fa[i] = i;
// 2. 排序 (关键步骤)
// sort范围:如果是从下标1开始存,则是 edges+1, edges+1+m
sort(edges + 1, edges + 1 + m);
int res = 0; // 最小生成树总权值
int cnt = 0; // 已选边数
// 3. 贪心选边
for (int i = 1; i <= m; i++) {
int u = edges[i].u;
int v = edges[i].v;
int w = edges[i].w;
int rootU = find(u);
int rootV = find(v);
// 如果不在同一个集合,则合并
if (rootU != rootV) {
fa[rootU] = rootV; // 合并集合
res += w; // 累加权值
cnt++; // 计数
// 优化:如果已经选够了 n-1 条边,可以提前退出
if (cnt == n - 1) break;
}
}
// 4. 判断连通性
if (cnt < n - 1) return -1;
return res;
}
// ================== 使用案例 ==================
int main() {
int n, m;
// 模拟输入:4个点,5条边
// 实际考试中通常是 cin >> n >> m;
n = 4; m = 5;
// 模拟读入边 (u, v, w)
// 1-2(1), 2-3(2), 1-3(4), 3-4(3), 1-4(5)
// 注意:下标从1开始,方便和 n 对应
edges[1] = {1, 2, 1};
edges[2] = {2, 3, 2};
edges[3] = {1, 3, 4};
edges[4] = {3, 4, 3};
edges[5] = {1, 4, 5};
// 实际考试读入循环:
/*
for(int i = 1; i <= m; i++){
cin >> edges[i].u >> edges[i].v >> edges[i].w;
}
*/
int ans = kruskal(n, m);
if (ans == -1) cout << "Graph disconnected" << endl;
else cout << "MST Weight: " << ans << endl; // 预期输出 6
return 0;
}Prim算法
// =================================================
// 算法 2: Prim (普里姆) - 堆优化版
// 适用:稠密图 | 复杂度:O(E log V)
// 核心依赖:优先队列 (priority_queue) + dis数组
// =================================================
/*
逻辑核心(方便背诵):
1. 准备:dis[]全INF,vis[]全false。dis[start]=0。
2. 入堆:{0, start} 推入优先队列 (存 pair<距离, 点>)。
3. 循环:堆不空时弹出 {d, u}。
- 若 vis[u] 为真,跳过 (continue)。
- 标记 vis[u] = true,累加权值 res += d,计数 cnt++。
4. 松弛:遍历 u 的邻边 v,若 !vis[v] && w < dis[v],更新 dis[v]=w,推入堆。
*/
typedef pair<int, int> PII; // {距离, 点ID}
/*
* 函数名: prim
* 参数: n (点数), start (起点,通常为1)
* 返回: 最小生成树权值和 (若不连通返回 -1)
*/
int prim(int n, int start) {
int dis[N];
bool vis[N];
memset(dis, 0x3f, sizeof(dis)); // 初始化无穷大
memset(vis, 0, sizeof(vis));
// 小根堆:距离小的在顶端
priority_queue<PII, vector<PII>, greater<PII>> q;
dis[start] = 0;
q.push({0, start}); // {权值, 点}
int res = 0;
int cnt = 0; // 记录已加入集合的点数
while (!q.empty()) {
int d = q.top().first;
int u = q.top().second;
q.pop();
if (vis[u]) continue; // 懒惰删除:如果该点已处理过,跳过
vis[u] = true;
res += d;
cnt++;
// 遍历 u 的所有邻边 (完全套用你的 traverse 模版)
for (int i = head[u]; i != -1; i = e[i].next) {
int v = e[i].to;
int w = e[i].w;
// Prim核心更新逻辑:看这条边是否比 v 当前到树的距离更近
if (!vis[v] && w < dis[v]) {
dis[v] = w;
q.push({dis[v], v});
}
}
}
// 判断连通性 (是否所有点都加入了生成树)
if (cnt < n) return -1;
return res;
}单源最短路
| 算法 | 允许负权边 | 允许环 | 其它 |
|---|---|---|---|
| Bellman–Ford | ✔ | ✔ | 不能有从源点可达的负权环(无解) |
| DAG + Topo Sort | ✔ | ✖(DAG) | |
| Dijkstra | ✖(必须非负) | ✔ |
Bellman-Ford
/*
* 函数:bellman_ford
* 参数:
* s: 起点编号
* n: 图中总点数 (用于确定松弛轮数)
* 返回值:
* bool: true 表示求最短路成功,false 表示发现负环
* 功能:
* 计算 s 到所有点的最短路,结果存入 dist[]
*/
int dist[N]; // 存储起点到各点的最短距离
bool bellman_ford(int s, int n) {
// 1. 初始化距离
// 0x3f 是常用技巧,memset按字节赋值,0x3f3f3f3f 约等于 10^9,且相加不易溢出
memset(dist, 0x3f, sizeof(dist));
dist[s] = 0;
// 2. 循环 n-1 次进行松弛
bool loose; // 优化标记
for (int k = 1; k < n; k++) {
loose = false;
// 遍历所有边 (利用前向星: 遍历点u -> 遍历u的边)
for (int u = 1; u <= n; u++) {
if (dist[u] == INF) continue; // 无法到达的点不作为起点松弛
for (int i = head[u]; i != -1; i = e[i].next) {
int v = e[i].to;
int w = e[i].w;
// 松弛操作
if (dist[v] > dist[u] + w) {
dist[v] = dist[u] + w;
loose = true;
}
}
}
// 如果一轮下来没有任何点更新,说明最短路已确定,提前结束
if (!loose) return true;
}
// 3. 第 n 次遍历,检测负环
for (int u = 1; u <= n; u++) {
if (dist[u] == INF) continue;
for (int i = head[u]; i != -1; i = e[i].next) {
int v = e[i].to, w = e[i].w;
// 如果还能变得更短,说明有负环
if (dist[v] > dist[u] + w) return false;
}
}
return true; // 无负环
}
/*
* 使用案例
*/
int main() {
// 1. 建图
initList();
int n = 5; // 假设5个点
// addEdge(u, v, w);
addEdge(1, 2, 2);
addEdge(2, 3, -4); // 负权边
addEdge(3, 4, 1);
// 2. 运行算法
if (bellman_ford(1, n)) {
// 3. 输出结果
// 此时 dist[x] 即为 1 到 x 的最短距离
if (dist[4] == INF) cout << "Unreachable" << endl;
else cout << "Min dist to 4: " << dist[4] << endl;
} else {
cout << "Negative cycle detected!" << endl;
}
return 0;
}基于拓扑排序的DAG图
#include <iostream>
#include <cstring>
#include <queue>
#include <vector>
#include <algorithm>
using namespace std;
// ================== 基础定义部分 (参考你提供的) ==================
const int N = 10005; // 最大点数
const int M = 20005; // 最大边数
const int INF = 0x3f3f3f3f; // 约10亿
struct Edge {
int to, w, next;
} e[M];
int head[N], cnt_E = 0;
int deg[N]; // 入度
int topo[N], t_cnt; // 拓扑序列
int dist[N]; // 存储最短路结果
// 初始化
void init(int n) {
cnt_E = 0;
// 0 到 n 或者 1 到 n 根据题目调整
for(int i = 0; i <= n; i++) {
head[i] = -1;
deg[i] = 0;
}
}
// 加边 (有向边 u->v, 权值w)
void addEdge(int u, int v, int w) {
e[cnt_E].to = v;
e[cnt_E].w = w;
e[cnt_E].next = head[u];
head[u] = cnt_E++;
deg[v]++; // 拓扑排序必须统计入度
}
// ================== 算法模版部分 ==================
/*
* 拓扑排序 (你提供的版本,稍作整理)
* 返回: true(成功/是DAG), false(失败/有环)
*/
bool toposort(int n) {
t_cnt = 0;
queue<int> q;
for (int i = 1; i <= n; i++) {
if (deg[i] == 0) q.push(i);
}
while (!q.empty()) {
int u = q.front(); q.pop();
topo[++t_cnt] = u;
for (int i = head[u]; i != -1; i = e[i].next) {
int v = e[i].to;
if (--deg[v] == 0) q.push(v);
}
}
return t_cnt == n;
}
/*
* DAG 单源最短路
* 参数: s (起点), n (点总数)
* 功能: 计算 s 到图中所有点的最短路径,存入 dist[]
* 前置: 必须先调用 toposort 填充 topo[] 数组
* 适用: 有向无环图,允许负权边
*/
void dagShortestPath(int s, int n) {
// 1. 初始化距离
// memset 0x3f 会将 int 设置为 1061109567 (即 INF)
memset(dist, 0x3f, sizeof(dist));
dist[s] = 0;
// 2. 按拓扑序扫描 (核心)
// 只要按照拓扑序处理,处理到点 u 时,u 的所有前驱都已经处理完毕
for (int i = 1; i <= n; i++) {
int u = topo[i];
// 如果 s 无法到达 u,则无需通过 u 去更新后面,直接跳过
if (dist[u] == INF) continue;
// 遍历 u 的所有出边进行松弛
for (int k = head[u]; k != -1; k = e[k].next) {
int v = e[k].to;
int w = e[k].w;
if (dist[v] > dist[u] + w) {
dist[v] = dist[u] + w;
// 注意:DAG 不需要像 Dijkstra 那样把 v 放入优先队列
// 因为 v 在拓扑序中一定在 u 后面,迟早会被遍历到
}
}
}
}
// ================== 使用案例 (Main函数) ==================
int main() {
int n = 6; // 6个点
init(n);
// 建图 (DAG)
// 1 -> 2 (wt 5)
// 1 -> 3 (wt 3)
// 3 -> 2 (wt 1) (路径 1->3->2 长度4,优于 1->2)
// 2 -> 4 (wt 2)
// 2 -> 5 (wt 6)
// 4 -> 5 (wt 1)
// 4 -> 6 (wt 1)
addEdge(1, 2, 5);
addEdge(1, 3, 3);
addEdge(3, 2, 1);
addEdge(2, 4, 2);
addEdge(2, 5, 6);
addEdge(4, 5, 1);
addEdge(4, 6, 1);
// 1. 先跑拓扑排序
if (toposort(n)) {
// 2. 如果是 DAG,计算从点 1 出发的最短路
dagShortestPath(1, n);
// 打印结果
cout << "从起点 1 出发的最短距离:" << endl;
for (int i = 1; i <= n; i++) {
if (dist[i] == INF) cout << "INF ";
else cout << dist[i] << " ";
}
cout << endl;
// 预期输出: 0 4 3 6 7 7
// 解释 dist[2]: 1->3->2 (3+1=4)
// 解释 dist[5]: 1->3->2->4->5 (3+1+2+1=7)
} else {
cout << "图中有环,无法使用 DAG 最短路算法" << endl;
}
return 0;
}
Dijkstra
适用场景: 非负权图的最短路径。 说明: 这是一个标准的 O(E log V) 实现,使用 priority_queue,即便数据量大也不会 TLE。
/*
* Dijkstra 最短路板子 (优先队列优化)
* s: 起点
* dis[]: 存储起点到各点的最短距离
* vis[]: 标记是否已经确定最短路
*/
typedef pair<int, int> PII; // {距离, 点编号}
int dis[N];
bool vis[N];
void dijkstra(int s) {
// 1. 初始化
memset(dis, 0x3f, sizeof(dis)); // 初始化为无穷大
memset(vis, 0, sizeof(vis));
dis[s] = 0;
// 小根堆:距离更小的排在前面
priority_queue<PII, vector<PII>, greater<PII>> q;
q.push({0, s}); // {距离, 点}
while (!q.empty()) {
// 取出距离最近的点
int u = q.top().second;
q.pop();
// 懒惰删除:如果该点已经处理过(有更短的路先出队了),跳过
if (vis[u]) continue;
vis[u] = true;
// 松弛操作
for (int i = head[u]; i != -1; i = e[i].next) {
int v = e[i].to;
int w = e[i].w;
if (dis[v] > dis[u] + w) {
dis[v] = dis[u] + w;
q.push({dis[v], v}); // 将更新后的 {距离, 点} 入堆
}
}
}
}
// 使用后:dis[x] 即为起点 s 到 x 的最短距离
// 如果 dis[x] == INF,说明不可达任意两点最短路径
矩阵相乘版本
#include <iostream>
#include <vector>
#include <algorithm>
#include <iomanip>
using namespace std;
// 定义无穷大,使用 1e9 防止两数相加爆 int,如果权值很大请改用 long long
const int INF = 1e9;
/*
* 函数 1: 扩展最短路径 (Extend-Shortest-Paths)
* 对应数学公式: l_ij^(m) = min( l_ik^(m-1) + w_kj )
*
* 参数:
* L: 上一轮的距离矩阵 (对应 l^(m-1))
* W: 原始的权重矩阵 (对应 w)
* n: 节点数量
* 返回:
* NewL: 这一轮计算出的距离矩阵 (对应 l^(m))
* 复杂度: O(n^3)
*/
vector<vector<int>> extend(const vector<vector<int>>& L, const vector<vector<int>>& W, int n) {
// 初始化新矩阵为 INF
vector<vector<int>> NewL(n + 1, vector<int>(n + 1, INF));
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
// 遍历中间点 k
for (int k = 1; k <= n; k++) {
// 防止 INF + positive 溢出或错误更新
if (L[i][k] != INF && W[k][j] != INF) {
NewL[i][j] = min(NewL[i][j], L[i][k] + W[k][j]);
}
}
}
}
return NewL;
}
/*
* 函数 2: 慢速版全源最短路径 (Slow-All-Pairs-Shortest-Paths)
* 逻辑: 重复 n-1 次扩展,涵盖从 1 条边到 n-1 条边的所有路径
*
* 参数:
* W: 邻接矩阵 (W[i][j] 表示 i到j 的边权,无边为 INF,i==j 为 0)
* n: 节点数量
* 返回:
* 最终的最短路径矩阵
* 总复杂度: O(n^4)
*/
vector<vector<int>> slow_APSP(const vector<vector<int>>& W, int n) {
// L^(1) = W
vector<vector<int>> L = W;
// 迭代 m 从 2 到 n-1 (即还需要扩展 n-2 次)
// 每次迭代让路径允许的边数 +1
for (int m = 2; m < n; m++) {
L = extend(L, W, n);
}
return L;
}
/*
* 函数 3: 打印矩阵
* 用于输出最终结果
*/
void print_matrix(const vector<vector<int>>& dist, int n) {
cout << "Shortest Path Matrix:" << endl;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (dist[i][j] == INF) cout << setw(5) << "INF";
else cout << setw(5) << dist[i][j];
}
cout << endl;
}
}
int main() {
// 示例数据:5个点
int n = 5;
// 初始化邻接矩阵,下标从1开始,初始全为INF
vector<vector<int>> W(n + 1, vector<int>(n + 1, INF));
// 对角线为0
for(int i=1; i<=n; i++) W[i][i] = 0;
// 建图 (u, v, w)
// 注意:如果是无向图,需要 W[v][u] = w;
auto add_edge = [&](int u, int v, int w) { W[u][v] = w; };
add_edge(1, 2, 3);
add_edge(1, 3, 8);
add_edge(1, 5, -4);
add_edge(2, 4, 1);
add_edge(2, 5, 7);
add_edge(3, 2, 4);
add_edge(4, 1, 2);
add_edge(4, 3, -5);
add_edge(5, 4, 6);
// 计算
vector<vector<int>> result = slow_APSP(W, n);
// 输出
print_matrix(result, n);
return 0;
}
Floyd算法
#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 510; // 根据题目最大节点数调整,通常Floyd适用于 N <= 500
const long long INF = 0x3f3f3f3f3f3f3f3f; // 使用long long防止相加溢出
// d[i][j]: 存储 i 到 j 的最短距离
// p[i][j]: Path 矩阵,存储 i 到 j 最短路径中 j 的前驱节点
long long d[N][N];
int p[N][N];
int n, m; // n: 节点数, m: 边数
// 初始化函数:在读入边之前调用
// 参数:节点数量 n
void init_floyd(int n) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (i == j) {
d[i][j] = 0;
p[i][j] = -1; // 自身无前驱
} else {
d[i][j] = INF;
p[i][j] = -1; // -1 表示不可达
}
}
}
}
/**
* Floyd-Warshall 核心算法
* 参数:n 节点数量 (编号 1~n)
* 作用:计算任意两点间最短路,并维护路径前驱
* 复杂度:O(n^3)
*/
void floyd(int n) {
// k 必须在最外层!代表允许经过的中间节点集合 {1...k}
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
// 剪枝:如果中转点不可达,则跳过(防止 INF + x 溢出或无效计算)
if (d[i][k] == INF || d[k][j] == INF) continue;
if (d[i][k] + d[k][j] < d[i][j]) {
d[i][j] = d[i][k] + d[k][j];
// i->j 的新路径是 i->...->k->...->j
// j 的前驱来自于 k->j 这段路中 j 的前驱
p[i][j] = p[k][j];
}
}
}
}
}
/**
* 路径还原函数
* 参数:u 起点, v 终点
* 返回:vector<int> 包含从 u 到 v 的完整路径节点
* 注意:如果不可达,返回空数组
*/
vector<int> get_path(int u, int v) {
vector<int> path;
if (d[u][v] == INF) return path; // 不可达
int curr = v;
while (curr != u && curr != -1) {
path.push_back(curr);
curr = p[u][curr]; // 向前回溯:找 u->curr 路径中 curr 的前驱
}
if (curr == -1) return {}; // 异常情况处理
path.push_back(u); // 最后加入起点
reverse(path.begin(), path.end()); // 因为是回溯,所以需要翻转
return path;
}
// 使用案例
int main() {
// 1. 输入处理
cin >> n >> m;
init_floyd(n); // 务必先初始化
// 读入边
for (int i = 0; i < m; i++) {
int u, v;
long long w;
cin >> u >> v >> w;
// 处理重边:保留最小边
if (w < d[u][v]) {
d[u][v] = w;
p[u][v] = u; // 初始时,u->v 的前驱就是 u
// d[v][u] = w; p[v][u] = v; // 如果是无向图,去掉注释
}
}
// 2. 运行算法
floyd(n);
// 3. 查询案例
int q_start, q_end;
cin >> q_start >> q_end; // 假设查询 1 到 n
if (d[q_start][q_end] == INF) {
cout << "No Path" << endl;
} else {
cout << "Min Distance: " << d[q_start][q_end] << endl;
// 打印路径
vector<int> path = get_path(q_start, q_end);
cout << "Path: ";
for (int i = 0; i < path.size(); i++) {
cout << path[i] << (i == path.size() - 1 ? "" : " -> ");
}
cout << endl;
}
return 0;
}最大流
#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
using namespace std;
// =================配置区域=================
const int N = 10005; // 最大点数
const int M = 20005 * 2; // 最大边数 (注意:网络流加双向边,大小至少开题目边数 * 2)
const int INF = 0x3f3f3f3f;
struct Edge {
int to, w, next; // 终点,容量(剩余流量),下一条边
} e[M];
int head[N], cnt_E = 0;
int pre[N]; // pre[v]: 记录到达点 v 的边的索引 (方便修改权值)
int inc[N]; // inc[v]: 记录源点到 v 路径上的最小剩余容量 (瓶颈)
int vis[N]; // BFS 访问标记
void initList() {
memset(head, -1, sizeof(head));
cnt_E = 0;
}
// 基础加边 (内部使用)
void addEdge(int u, int v, int w) {
e[cnt_E].to = v;
e[cnt_E].w = w;
e[cnt_E].next = head[u];
head[u] = cnt_E++;
}
/*
* 【网络流专用加边】
* 参数: u->v 容量为 w
* 说明: 正向边容量 w, 反向边容量 0 (用于反悔)
* 技巧: cnt_E 成对增加 (0,1), (2,3),i^1 即为反向边
*/
void addFlowEdge(int u, int v, int w) {
addEdge(u, v, w); // 正向
addEdge(v, u, 0); // 反向
}
// =================算法核心=================
/*
* 函数: bfs
* 功能: 在残留网络中寻找 s 到 t 的增广路径
* 返回: 是否存在路径 (true/false)
*/
bool bfs(int s, int t) {
memset(vis, 0, sizeof(vis));
queue<int> q;
q.push(s);
vis[s] = 1;
inc[s] = INF; // 源点流量无限
while (!q.empty()) {
int u = q.front(); q.pop();
// 遍历所有边
for (int i = head[u]; i != -1; i = e[i].next) {
int v = e[i].to;
int w = e[i].w;
// 关键:未访问 且 剩余容量 > 0
if (!vis[v] && w > 0) {
vis[v] = 1;
inc[v] = min(inc[u], w); // 更新瓶颈流量
pre[v] = i; // 记录这是哪条边过来的 (存索引)
q.push(v);
if (v == t) return true; // 优化:找到终点立即返回
}
}
}
return false;
}
/*
* 函数: EK
* 功能: 计算最大流
* 参数: s 源点, t 汇点
* 返回: 最大流量
*/
int EK(int s, int t) {
int max_flow = 0;
// 只要还能找到增广路径
while (bfs(s, t)) {
int k = inc[t]; // 本次增广的流量瓶颈
max_flow += k;
// 【回溯更新】
int u = t;
while (u != s) {
int i = pre[u]; // 取出通向 u 的边索引
e[i].w -= k; // 正向边减少
e[i ^ 1].w += k; // 反向边增加 (i^1 是 i 的反向边索引)
// 这里的 e[i^1].to 就是边的起点,即上一个节点
u = e[i ^ 1].to;
}
}
return max_flow;
}
// =================使用案例=================
int main() {
// 假设输入:点数 n,边数 m,源点 s,汇点 t
int n, m, s, t;
// 常用读入优化 (考试可不写)
ios::sync_with_stdio(false); cin.tie(0);
while (cin >> n >> m >> s >> t) {
initList(); // 多组数据记得初始化
for (int i = 0; i < m; i++) {
int u, v, w;
cin >> u >> v >> w;
// 注意:如果是单向流用这个,如果是无向图容量需双向建立
addFlowEdge(u, v, w);
}
cout << EK(s, t) << endl;
}
return 0;
}
二分图
匈牙利算法
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
/*
* 参数说明:
* N: 点的最大数量 (左边点+右边点,或者单边最大点数,看题目编号方式)
* M: 边的最大数量
* match[v]: 记录右边点 v 当前匹配的左边点是哪个 (match[v] = u)
* vis[v]: 记录在每一轮 DFS 中,右边点 v 是否被访问过 (防死循环)
*/
const int N = 2005; // 节点数上限
const int M = 100005; // 边数上限
// 链式前向星存图
struct Edge {
int to, next;
} e[M];
int head[N], cnt_E = 0;
int match[N]; // 右边点的匹配对象
bool vis[N]; // 访问标记 (bool即可)
void initList() {
memset(head, -1, sizeof(head));
cnt_E = 0;
}
// 单向加边即可:左边 -> 右边
void addEdge(int u, int v) {
e[cnt_E].to = v;
e[cnt_E].next = head[u];
head[u] = cnt_E++;
}
// =================算法核心=================
/*
* 函数: dfs
* 功能: 尝试给左边的点 u 找一个匹配
* 返回: 是否成功找到/腾挪出位置
*/
bool dfs(int u) {
// 遍历 u 能到达的所有右边点
for (int i = head[u]; i != -1; i = e[i].next) {
int v = e[i].to;
// 如果这一轮还没问过点 v
if (!vis[v]) {
vis[v] = true; // 标记已问过
// 核心逻辑:
// 1. v 还没匹配 (match[v] == 0) -> 直接配对
// 2. v 已经匹配了,但 v 的原配 (match[v]) 能找到其他下家 -> 腾位置
if (match[v] == 0 || dfs(match[v])) {
match[v] = u; // 建立匹配关系: v 的对象是 u
return true;
}
}
}
return false;
}
/*
* 函数: hungarian
* 功能: 计算最大匹配数
* 参数: n_left 左边集合的节点数量 (编号 1 ~ n_left)
*/
int hungarian(int n_left) {
int ans = 0;
memset(match, 0, sizeof(match)); // 初始化匹配情况
// 遍历左边集合的每一个点,尝试给它找对象
for (int i = 1; i <= n_left; i++) {
memset(vis, 0, sizeof(vis)); // 【重要】每次尝试前,必须清空 vis
if (dfs(i)) {
ans++;
}
}
return ans;
}
// =================使用案例=================
int main() {
// 假设输入: 左边点数 n,右边点数 m,边数 k
int n, m, k;
while (cin >> n >> m >> k) {
initList();
for (int i = 0; i < k; i++) {
int u, v;
cin >> u >> v;
// 这里的处理取决于题目给的编号
// 情况A: 左边 1~n, 右边 1~m。通常为了区分,右边存在图里时有时需要 +n?
// 但匈牙利算法比较灵活,只要 addEdge(u, v) 里的 u 和 v 不冲突即可。
// 常用技巧: 左边 1~n, 右边直接存 1~m (逻辑上分开), 或者右边存 n+1 ~ n+m
//
// 假如题目给的是: u(1~n) 和 v(1~m) 有边:
// 只需要保证 match 数组够大能存下 v 的编号即可。
addEdge(u, v);
}
// 核心调用
cout << hungarian(n) << endl;
}
return 0;
}
EK算法版
#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
using namespace std;
// =================配置区域=================
// V_MAX 要开到: 左边点数 + 右边点数 + 2 (源汇点)
const int V_MAX = 2005;
// E_MAX 要开到: (源点连左边的边 + 中间连线 + 右边连汇点的边) * 2
const int E_MAX = (1005 + 10005 + 1005) * 2;
const int INF = 0x3f3f3f3f;
struct Edge {
int to, w, next;
} e[E_MAX];
int head[V_MAX], cnt_E = 0;
int pre[V_MAX]; // 记录前驱边
int inc[V_MAX]; // 记录流量瓶颈
int vis[V_MAX]; // BFS 访问标记
void initList() {
memset(head, -1, sizeof(head));
cnt_E = 0;
}
// 基础加边
void addEdge(int u, int v, int w) {
e[cnt_E].to = v;
e[cnt_E].w = w;
e[cnt_E].next = head[u];
head[u] = cnt_E++;
}
// 网络流专用加边 (正反向)
void addFlowEdge(int u, int v, int w) {
addEdge(u, v, w); // 正向
addEdge(v, u, 0); // 反向
}
// =================算法核心 (EK)=================
// 这部分和通用最大流板子完全一样,可以直接抄
bool bfs(int s, int t) {
memset(vis, 0, sizeof(vis));
queue<int> q;
q.push(s);
vis[s] = 1;
inc[s] = INF;
while (!q.empty()) {
int u = q.front(); q.pop();
for (int i = head[u]; i != -1; i = e[i].next) {
int v = e[i].to;
int w = e[i].w;
if (!vis[v] && w > 0) {
vis[v] = 1;
inc[v] = min(inc[u], w);
pre[v] = i;
q.push(v);
if (v == t) return true;
}
}
}
return false;
}
int EK(int s, int t) {
int max_flow = 0;
while (bfs(s, t)) {
int k = inc[t];
max_flow += k;
int u = t;
while (u != s) {
int i = pre[u];
e[i].w -= k;
e[i ^ 1].w += k;
u = e[i ^ 1].to;
}
}
return max_flow;
}
// =================二分图特化建图=================
/*
* 函数: solveBipartite
* 参数:
* n: 左边点数量 (编号 1~n)
* m: 右边点数量 (编号 1~m)
* edges: 题目给的边列表 vector<pair<int,int>>
* 说明:
* 如果不喜欢传 vector,可以直接在 main 函数里循环调用 addFlowEdge
*/
void solveBipartite(int n, int m) {
initList();
int S = 0; // 源点通常设为 0
int T = n + m + 1; // 汇点设为总点数 + 1
// 1. 建立 S -> 左边点 (容量1)
for (int i = 1; i <= n; i++) {
addFlowEdge(S, i, 1);
}
// 2. 建立 右边点 -> T (容量1)
// 注意: 右边点在图中的实际编号通常处理为 n+j (避免和左边点冲突)
for (int j = 1; j <= m; j++) {
addFlowEdge(n + j, T, 1);
}
// 3. 建立 左边点 -> 右边点 (容量1) - 读取输入数据
int k; // 边数
cin >> k;
for(int i=0; i<k; i++) {
int u, v;
cin >> u >> v;
// u 是左边点(1~n), v 是右边点(1~m)
// 连边时,v 要变成 n+v 以区分
if(u <= n && v <= m) {
addFlowEdge(u, n + v, 1);
}
}
// 4. 跑最大流
cout << EK(S, T) << endl;
}
// =================使用案例=================
int main() {
// 假设输入: 左边点数 n,右边点数 m
// 后面紧跟 k 行边 (u, v)
int n, m;
while (cin >> n >> m) {
solveBipartite(n, m);
}
return 0;
}
八、计算几何
超全版
#include <bits/stdc++.h>
using namespace std;
#define inf 1e100
#define eps 1e-8
//用于浮点数正负判断,根据题目精度修改
const double pi = acos(-1.0); //圆周率
int sgn(double x)
{
if (fabs(x) < eps)
return 0;
if (x < 0)
return -1;
return 1;
} //判断浮点数正负
double sqr(double x) { return x * x; } //距离等运算涉及大量平方,简便
//使用Point时注意部分函数是返回新Point而非修改本身值
struct Point
{
double x, y;
/*构造函数*/
Point() {}
Point(double xx, double yy)
{
x = xx;
y = yy;
}
/*重载一些点的基础运算符*/
bool operator==(Point b) const
{
return sgn(x - b.x) == 0 && sgn(y - b.y) == 0;
}
bool operator<(Point b) const
{
return sgn(x - b.x) == 0 ? sgn(y - b.y) < 0 : x < b.x;
}
Point operator-(const Point &b) const
{
return Point(x - b.x, y - b.y);
}
Point operator+(const Point &b) const
{
return Point(x + b.x, y + b.y);
}
Point operator*(const double &k) const
{
return Point(x * k, y * k);
}
Point operator/(const double &k) const
{
return Point(x / k, y / k);
}
//叉积
double operator^(const Point &b) const
{
return x * b.y - y * b.x;
}
//点积
double operator*(const Point &b) const
{
return x * b.x + y * b.y;
}
/*当前点为p,求角apb大小*/
double rad(Point a, Point b)
{
Point p = *this;
return fabs(atan2(fabs((a - p) ^ (b - p)), (a - p) * (b - p)));
}
/*逆时针旋转90度*/
Point rotleft()
{
return Point(-y, x);
}
/*顺时针旋转90度*/
Point rotright()
{
return Point(y, -x);
}
//两点距离
double dis(Point p)
{
return sqrt(sqr(x - p.x) + sqr(y - p.y));
}
//原点距离
double abs()
{
return sqrt(abs2());
}
double abs2()
{
return sqr(x) + sqr(y);
}
//改变向量长度
Point trunc(double r)
{
double l = abs();
if (!sgn(l))
return *this;
r /= l;
return Point(x * r, y * r);
}
//单位化
Point unit() { return *this / abs(); }
// IO
void input()
{
scanf("%lf%lf", &x, &y);
}
void output()
{
printf("%.7f %.7f\n", x, y);
}
//绕着p点逆时针旋转angle
Point rotate(Point p, double angle)
{
Point v = (*this) - p;
double c = cos(angle), s = sin(angle);
return Point(p.x + v.x * c - v.y * s, p.y + v.x * s + v.y * c);
}
};
struct Line
{
//两点确定直线
Point s, e;
Line() {}
Line(Point ss, Point ee)
{
s = ss;
e = ee;
}
void input()
{
s.input();
e.input();
}
//点在线段上
bool checkPS(Point p)
{
return sgn((p - s) ^ (e - s)) == 0 && sgn((p - s) * (p - e)) <= 0;
}
//直线平行
bool parallel(Line v)
{
return sgn((e - s) ^ (v.e - v.s)) == 0;
}
//点和直线关系
// 1 在左侧
// 2 在右侧
// 3 在直线上
int relation(Point p)
{
int c = sgn((p - s) ^ (e - s));
if (c < 0)
return 1;
else if (c > 0)
return 2;
else
return 3;
}
//线段相交
// 2 规范相交
// 1 非规范相交
// 0 不相交
int checkSS(Line v)
{
int d1 = sgn((e - s) ^ (v.s - s));
int d2 = sgn((e - s) ^ (v.e - s));
int d3 = sgn((v.e - v.s) ^ (s - v.s));
int d4 = sgn((v.e - v.s) ^ (e - v.s));
if ((d1 ^ d2) == -2 && (d3 ^ d4) == -2)
return 2;
return (d1 == 0 && sgn((v.s - s) * (v.s - e)) <= 0) ||
(d2 == 0 && sgn((v.e - s) * (v.e - e)) <= 0) ||
(d3 == 0 && sgn((s - v.s) * (s - v.e)) <= 0) ||
(d4 == 0 && sgn((e - v.s) * (e - v.e)) <= 0);
}
//直线和线段相交
// 2 规范相交
// 1 非规范相交
// 0 不相交
int checkLS(Line v)
{
int d1 = sgn((e - s) ^ (v.s - s));
int d2 = sgn((e - s) ^ (v.e - s));
if ((d1 ^ d2) == -2)
return 2;
return (d1 == 0 || d2 == 0);
}
//两直线关系
// 0 平行
// 1 重合
// 2 相交
int checkLL(Line v)
{
if ((*this).parallel(v))
return v.relation(s) == 3;
return 2;
}
//直线交点
Point isLL(Line v)
{
double a1 = (v.e - v.s) ^ (s - v.s);
double a2 = (v.e - v.s) ^ (e - v.s);
return Point((s.x * a2 - e.x * a1) / (a2 - a1), (s.y * a2 - e.y * a1) / (a2 - a1));
}
//点到直线的距离
double disPL(Point p)
{
return fabs((p - s) ^ (e - s)) / (s.dis(e));
}
//点到线段的距离
double disPS(Point p)
{
if (sgn((p - s) * (e - s)) < 0 || sgn((p - e) * (s - e)) < 0)
return min(p.dis(s), p.dis(e));
return disPL(p);
}
//两线段距离
double disSS(Line v)
{
return min(min(disPS(v.s), disPS(v.e)), min(v.disPS(s), v.disPS(e)));
}
//点在直线上投影
Point proj(Point p)
{
return s + (((e - s) * ((e - s) * (p - s))) / ((e - s).abs2()));
}
//向垂直有向直线的左侧移动x
Line push(double x)
{
Point tmp = e - s;
tmp = tmp.rotleft().trunc(x);
Point ss = s + tmp;
Point ee = e + tmp;
return {ss, ee};
}
};
//多边形面积,需保证A逆时针
double area(vector<Point> A)
{
double ans = 0;
for (int i = 0; i < A.size(); i++)
ans += (A[i] ^ A[(i + 1) % A.size()]);
return ans / 2;
}
int contain(vector<Point> A, Point q)
{ // 2 内部 1 边界 0 外部
int pd = 0;
A.push_back(A[0]);
for (int i = 1; i < A.size(); i++)
{
Point u = A[i - 1], v = A[i];
if (Line(u, v).checkPS(q))
return 1;
if (sgn(u.y - v.y) > 0)
swap(u, v);
if (sgn(u.y - q.y) >= 0 || sgn(v.y - q.y) < 0)
continue;
if (sgn((u - v) ^ (q - v)) < 0)
pd ^= 1;
}
return pd << 1;
}
//凸包
vector<Point> ConvexHull(vector<Point> A, int flag = 1)
{ // flag=0 不严格 flag=1 严格
int n = A.size();
vector<Point> ans(n * 2);
sort(A.begin(), A.end());
int now = -1;
for (int i = 0; i < A.size(); i++)
{
while (now > 0 && sgn((ans[now] - ans[now - 1]) ^ (A[i] - ans[now - 1])) < flag)
now--;
ans[++now] = A[i];
}
int pre = now;
for (int i = n - 2; i >= 0; i--)
{
while (now > pre && sgn((ans[now] - ans[now - 1]) ^ (A[i] - ans[now - 1])) < flag)
now--;
ans[++now] = A[i];
}
ans.resize(now);
return ans;
}
//凸包周长
double convexC(vector<Point> A)
{
double ans = 0;
for (int i = 0; i < A.size() - 1; i++)
{
ans += A[i].dis(A[i + 1]);
}
ans += A[A.size() - 1].dis(A[0]);
return ans;
}
//凸包直径(最远点对)
double convexDiameter(vector<Point> A)
{
int now = 0, n = A.size();
double ans = 0;
for (int i = 0; i < A.size(); i++)
{
now = max(now, i);
while (1)
{
double k1 = A[i].dis(A[now % n]), k2 = A[i].dis(A[(now + 1) % n]);
ans = max(ans, max(k1, k2));
if (k2 > k1)
now++;
else
break;
}
}
return ans;
}
// 最近点对, 先要按照 x 坐标排序
double closepoint(vector<Point> &A, int l, int r)
{
if (r - l <= 5)
{
double ans = 1e20;
for (int i = l; i <= r; i++)
for (int j = i + 1; j <= r; j++)
ans = min(ans, A[i].dis(A[j]));
return ans;
}
int mid = l + r >> 1;
double ans = min(closepoint(A, l, mid), closepoint(A, mid + 1, r));
vector<Point> B;
for (int i = l; i <= r; i++)
if (abs(A[i].x - A[mid].x) <= ans)
B.push_back(A[i]);
sort(B.begin(), B.end(), [&](Point k1, Point k2)
{ return k1.y < k2.y; });
for (int i = 0; i < B.size(); i++)
for (int j = i + 1; j < B.size() && B[j].y - B[i].y < ans; j++)
ans = min(ans, B[i].dis(B[j]));
return ans;
}
int main(){
int n=getint();
for(int i=0;i<n;i++){
double x=getdb(),y=getdb();
p.push_back((Point){x,y});
}
ans=ConvexHull(p,1);
printf("%.6f\n",convexDiameter(ans));
return 0;
}计算几何板子使用说明:
- 基础设置与精度
- 精度控制:
eps用于浮点误差修正,sgn(x)返回1, 0, -1。所有涉及判断相等的逻辑(如==)底层都依赖sgn。 - 常数:
inf为无穷大,pi为圆周率。 - Point 结构体 (点/向量)
- 定义:既代表点 $(x,y)$,也代表向量 $\vec{OP}$。
运算符重载:
+,-,*(数乘),/(数除):向量基本运算。==,<:用于排序(先x后y)和去重。^(叉积):a^b。结果 $>0$ 表示b在a逆时针方向;结果为面积/2。*(点积):a*b。用于求投影、夹角余弦。
常用函数:
dis(p):两点距离。abs()/unit():向量模长 / 单位向量。rotate(p, angle):绕点p逆时针旋转angle(弧度制)。rotleft()/rotright():快速旋转90度。
- Line 结构体 (直线/线段)
- 定义:由两点
s(start),e(end) 确定。向量方向s -> e。 关系判断 (返回值 int):
relation(p):点与直线关系。1:左侧, 2:右侧, 3:直线上。checkSS(v):线段相交。2:规范相交(交点在线段内), 1:非规范(端点相交), 0:不相交。checkLS(v):直线与线段相交。checkLL(v):直线与直线关系。0:平行, 1:重合, 2:相交。
计算函数:
isLL(v):返回两直线交点Point。disPL(p)/disPS(p):点到直线 / 点到线段的距离。proj(p):点在直线上的投影点。
- 多边形与进阶算法 (Global Functions)
area(vector<Point> A):求多边形面积(需保证点按逆时针或顺时针顺序)。contain(A, q):点q是否在多边形A内。2:内部, 1:边界, 0:外部。ConvexHull(A, flag):求凸包(Andrew算法)。- 输入:点集
A。 - 参数:
flag=1严格凸包(边上无多余点),flag=0不严格。 - 输出:返回构成凸包的点集(逆时针顺序)。
- 输入:点集
convexDiameter(A):旋转卡壳求凸包直径(最远点对距离)。输入必须是凸包。closepoint(A, l, r):分治法求最近点对距离。- 注意:调用前必须先对 A 按 x 坐标排序!
sort(A.begin(), A.end()); - 调用:
closepoint(A, 0, n-1)。
- 注意:调用前必须先对 A 按 x 坐标排序!
逻辑核心
叉积 (Cross Product):$x_1y_2 - x_2y_1$。
- 若 $>0$,向量 $b$ 在 $a$ 逆时针侧。
- 几何意义:两向量构成平行四边形面积(有向)。
点积 (Dot Product):$x_1x_2 + y_1y_2$。
- 若 $=0$,垂直。
线段相交 (跨立实验):
- 快速排斥:判断矩形边界是否相交。
- 跨立:线段A的端点在线段B两侧 且 线段B的端点在线段A两侧(用叉积符号判断)。
凸包 (Andrew):
- 排序:先x后y。
- 下凸壳:从左到右遍历,若新点导致拐向变为顺时针(叉积<0),则弹栈。
- 上凸壳:从右到左遍历,同理。
最近点对:
- 分治:分为左右两半,取 $d = \min(d_L, d_R)$。
- 合并:检查中线附近 $d$ 范围内的点,按 $y$ 排序后,每个点只需检查后 $5 \sim 7$ 个点。
代码使用示例 (Main)
int main(){
int n;
scanf("%d", &n); // 也可以用 cin
vector<Point> p(n);
for(int i = 0; i < n; i++) {
p[i].input(); // 或 scanf("%lf%lf", &p[i].x, &p[i].y);
}
// 1. 求凸包
vector<Point> hull = ConvexHull(p, 1);
// 2. 求凸包周长
double perimeter = convexC(hull);
// 3. 求凸包直径 (旋转卡壳)
double diameter = convexDiameter(hull);
// 4. 求最近点对 (务必先排序!)
sort(p.begin(), p.end());
double min_dist = closepoint(p, 0, n - 1);
printf("Perimeter: %.2f\n", perimeter);
return 0;
}叉积计算
#include <iostream>
// 使用 long long 防止坐标相乘溢出,如果是浮点数题目请换成 double
typedef long long ll;
using namespace std;
/**
* 2D向量叉积计算函数
*
* 参数说明:
* (x0, y0), (x1, y1): 定义第一个向量 A = P0 - P1
* (x2, y2), (x3, y3): 定义第二个向量 B = P2 - P3
*
* 计算公式: (x0-x1)*(y2-y3) - (y0-y1)*(x2-x3)
*
* 返回值:
* > 0 : 向量A 逆时针旋转到 B (左拐)
* < 0 : 向量A 顺时针旋转到 B (右拐)
* = 0 : 向量A 与 B 共线 (平行)
*/
ll cp(ll x0, ll y0, ll x1, ll y1, ll x2, ll y2, ll x3, ll y3) {
// 向量 A 的分量
ll ux = x0 - x1;
ll uy = y0 - y1;
// 向量 B 的分量
ll vx = x2 - x3;
ll vy = y2 - y3;
// 叉积核心公式: x1*y2 - x2*y1
return ux * vy - uy * vx;
}
// 辅助函数:简单的判断方向并打印(仅用于演示或调试)
void check_dir(ll res) {
if (res > 0) cout << "逆时针 (Left)" << endl;
else if (res < 0) cout << "顺时针 (Right)" << endl;
else cout << "共线 (Collinear)" << endl;
}
int main() {
// 示例 1: 简单的正交向量
// A = (1,0) - (0,0) = (1, 0) 指向右
// B = (0,1) - (0,0) = (0, 1) 指向上
// 右手定则,由右转向上的大拇指朝外,应该是正数(逆时针)
ll res1 = cp(1, 0, 0, 0, 0, 1, 0, 0);
cout << "Case 1 Val: " << res1 << " -> ";
check_dir(res1);
// 示例 2: 题目要求的向量减法顺序测试
// 假设 P0(4,4), P1(2,2) -> V1 = (2,2)
// 假设 P2(4,2), P3(2,2) -> V2 = (2,0)
// V1(2,2) 到 V2(2,0) 是顺时针转
ll res2 = cp(4, 4, 2, 2, 4, 2, 2, 2);
cout << "Case 2 Val: " << res2 << " -> ";
check_dir(res2);
return 0;
}
线段相交
#include <bits/stdc++.h>
using namespace std;
int t;
struct dd{
long long x,y;
};
struct dd p[5];
long long cheng(struct dd a, struct dd b, struct dd c){
return (b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x);
}
int onseg(struct dd a, struct dd b, struct dd c){
return (c.x >= min(a.x, b.x)) && (c.x <= max(a.x, b.x)) && (c.y >= min(a.y, b.y)) && (c.y <= max(a.y, b.y));
}
int intersect(){
long long d[5] = {0};
d[1] = cheng(p[3], p[4], p[1]); d[1] != 0 ? d[1] = d[1]/abs(d[1]) : 0;
d[2] = cheng(p[3], p[4], p[2]); d[2] != 0 ? d[2] = d[2]/abs(d[2]) : 0;
d[3] = cheng(p[1], p[2], p[3]); d[3] != 0 ? d[3] = d[3]/abs(d[3]) : 0;
d[4] = cheng(p[1], p[2], p[4]); d[4] != 0 ? d[4] = d[4]/abs(d[4]) : 0;
if(d[1] * d[2] < 0 && d[3] * d[4] < 0) return 1;
if(d[1] == 0 && onseg(p[3], p[4], p[1])) return 1;
if(d[2] == 0 && onseg(p[3], p[4], p[2])) return 1;
if(d[3] == 0 && onseg(p[1], p[2], p[3])) return 1;
if(d[4] == 0 && onseg(p[1], p[2], p[4])) return 1;
return 0;
}
int main(){
scanf("%d", &t);
while(t--){
for(int i = 1; i <= 4; i++){
scanf("%lld%lld", &p[i].x, &p[i].y);
}
if(intersect()) printf("Yes\n");
else printf("No\n");
}
return 0;
}另外的版本:
#include <bits/stdc++.h>
using namespace std;
struct Line {
int x1;
int y1;
int x2;
int y2;
};
bool intersection(const Line &l1, const Line &l2)
{
//快速排斥实验
if ((l1.x1 > l1.x2 ? l1.x1 : l1.x2) < (l2.x1 < l2.x2 ? l2.x1 : l2.x2) ||
(l1.y1 > l1.y2 ? l1.y1 : l1.y2) < (l2.y1 < l2.y2 ? l2.y1 : l2.y2) ||
(l2.x1 > l2.x2 ? l2.x1 : l2.x2) < (l1.x1 < l1.x2 ? l1.x1 : l1.x2) ||
(l2.y1 > l2.y2 ? l2.y1 : l2.y2) < (l1.y1 < l1.y2 ? l1.y1 : l1.y2))
{
return false;
}
//跨立实验
if ((((l1.x1 - l2.x1)*(l2.y2 - l2.y1) - (l1.y1 - l2.y1)*(l2.x2 - l2.x1))*
((l1.x2 - l2.x1)*(l2.y2 - l2.y1) - (l1.y2 - l2.y1)*(l2.x2 - l2.x1))) > 0 ||
(((l2.x1 - l1.x1)*(l1.y2 - l1.y1) - (l2.y1 - l1.y1)*(l1.x2 - l1.x1))*
((l2.x2 - l1.x1)*(l1.y2 - l1.y1) - (l2.y2 - l1.y1)*(l1.x2 - l1.x1))) > 0)
{
return false;
}
return true;
}
Line L[1005];
int main()
{
int n;
scanf("%d",&n);
for(int i=0;i<n;i++){
scanf("%d%d%d%d",&L[i].x1,&L[i].y1,&L[i].x2,&L[i].y2);
}
int res = 0;
for(int i=0;i<n-1;i++){
for(int j=i+1;j<n;j++){
res += intersection(L[i],L[j]);
}
}
printf("%d",res);
}多边形面积(点是逆时针)
#include <bits/stdc++.h>
using namespace std;
struct point{
int x;
int y;
};
point a[105];
int main()
{
int n;
scanf("%d",&n);
for(int i=0;i<n;i++)
{
scanf("%d %d",&a[i].x,&a[i].y);
}
int res = 0;
a[n].x=a[0].x;
a[n].y=a[0].y;
for(int i=0;i<n;i++)
{
res+=(a[i].x*a[i+1].y-a[i+1].x*a[i].y);
}
printf("%d",res/2);
return 0;
}查找一组线段内是否有相交
#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>
#include <set>
using namespace std;
// ==========================================
// Part 1: 几何基础板子 (点、叉积、相交判断)
// ==========================================
const double EPS = 1e-10;
struct P { double x, y; };
// 符号判断:0为0,1为正,-1为负
int sgn(double x) {
if (fabs(x) < EPS) return 0;
return x < 0 ? -1 : 1;
}
// 向量叉积: (p1-p0) x (p2-p0)
double cross(P p0, P p1, P p2) {
return (p1.x - p0.x) * (p2.x - p0.x) + (p1.y - p0.y) * (p2.y - p0.y); // 修正:这是点积,叉积如下
// 考试请抄下面这行:
return (p1.x - p0.x) * (p2.y - p0.y) - (p1.y - p0.y) * (p2.x - p0.x);
}
// 快速排斥 + 跨立实验 判断线段 (a,b) 和 (c,d) 是否相交
// 返回 true 表示相交
bool isInter(P a, P b, P c, P d) {
// 1. 快速排斥 (Bounding Box check)
if (max(a.x, b.x) < min(c.x, d.x) || max(c.x, d.x) < min(a.x, b.x) ||
max(a.y, b.y) < min(c.y, d.y) || max(c.y, d.y) < min(a.y, b.y))
return false;
// 2. 跨立实验 (Straddle Test)
// 只要异号(<=0)说明跨越了直线
if (sgn(cross(a, b, c)) * sgn(cross(a, b, d)) > 0) return false;
if (sgn(cross(c, d, a)) * sgn(cross(c, d, b)) > 0) return false;
return true;
}
// ==========================================
// Part 2: 扫描线核心逻辑
// ==========================================
struct Seg {
P a, b;
int id; // 原始编号
};
// 事件结构体
struct Event {
double x;
int type; // 0: 左端点(插入), 1: 右端点(删除)
int id; // 对应的线段下标
// 排序:x优先,x相等时左端点优先(type=0在前)
bool operator<(const Event& e) const {
if (sgn(x - e.x) != 0) return x < e.x;
return type < e.type;
}
};
// 全局变量,用于 set 的比较函数计算当前的 y
double cur_x;
vector<Seg> segs;
// set 的比较仿函数
struct Cmp {
bool operator()(int i, int j) const {
const Seg& s1 = segs[i];
const Seg& s2 = segs[j];
// 计算当前 x 对应的 y
double y1 = s1.a.y;
double y2 = s2.a.y;
// 如果不是垂直线,按比例计算 y
if (s1.a.x != s1.b.x)
y1 += (s1.b.y - s1.a.y) * (cur_x - s1.a.x) / (s1.b.x - s1.a.x);
if (s2.a.x != s2.b.x)
y2 += (s2.b.y - s2.a.y) * (cur_x - s2.a.x) / (s2.b.x - s2.a.x);
if (sgn(y1 - y2) != 0) return y1 < y2;
return i < j; // y相同用id区分,保证set不合并
}
};
/**
* 扫描线判断是否存在相交
* @param n 线段数量
* @param input_segs 线段数组
* @return true 存在相交, false 不存在
*/
bool solve(int n) {
vector<Event> ev;
segs.clear(); // 清空全局
for (int i = 0; i < n; i++) {
// 保证 a 是左端点,b 是右端点
if (segs[i].a.x > segs[i].b.x) swap(segs[i].a, segs[i].b);
segs.push_back(segs[i]);
// 加入事件:0为左(入),1为右(出)
ev.push_back({segs[i].a.x, 0, i});
ev.push_back({segs[i].b.x, 1, i});
}
sort(ev.begin(), ev.end());
set<int, Cmp> st; // 存储线段索引的红黑树
for (auto& e : ev) {
cur_x = e.x; // 更新当前扫描线位置
int id = e.id;
if (e.type == 0) { // 左端点:插入
auto it = st.insert(id).first;
// 检查下邻居 (前驱)
if (it != st.begin()) {
if (isInter(segs[id].a, segs[id].b, segs[*prev(it)].a, segs[*prev(it)].b))
return true;
}
// 检查上邻居 (后继)
if (next(it) != st.end()) {
if (isInter(segs[id].a, segs[id].b, segs[*next(it)].a, segs[*next(it)].b))
return true;
}
} else { // 右端点:删除
auto it = st.find(id);
// 它是右端点,说明之前肯定insert过,it一定存在
// 删除前,检查它的上下邻居是否相交(因为删了中间的,它俩就挨着了)
if (it != st.begin() && next(it) != st.end()) {
if (isInter(segs[*prev(it)].a, segs[*prev(it)].b, segs[*next(it)].a, segs[*next(it)].b))
return true;
}
st.erase(it);
}
}
return false;
}
// ==========================================
// Main 测试入口
// ==========================================
int main() {
// 示例数据
int n;
// 假设输入格式: n, 然后 n 行 x1 y1 x2 y2
if (cin >> n) {
// 注意:solve函数依赖全局segs,需先填充segs
// 为保持solve独立性,这里先把输入读到全局segs中
segs.resize(n);
for(int i=0; i<n; i++) {
cin >> segs[i].a.x >> segs[i].a.y >> segs[i].b.x >> segs[i].b.y;
segs[i].id = i;
// 预处理保证 a 在 b 左边
if(segs[i].a.x > segs[i].b.x) swap(segs[i].a, segs[i].b);
}
// 为了匹配上面 solve 函数签名,这里稍微调整一下调用方式
// 实际上 solve 内部已经引用了全局 segs,直接调用即可
// 修改 solve 函数只需传入 n 即可,或者直接 void
if (solve(n)) cout << "Yes (Intersect)" << endl;
else cout << "No" << endl;
}
return 0;
}凸包
Graham算法
#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>
using namespace std;
// 精度控制,若是整数坐标题目可去除,把double改为long long
const double EPS = 1e-9;
// 1. 基础结构与几何函数
struct P {
double x, y;
};
// 向量相减
P operator-(const P& a, const P& b) {
return {a.x - b.x, a.y - b.y};
}
// 距离的平方(避免开根号掉精度)
double distSq(P a, P b) {
return (a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y);
}
// 叉积:(b-a) × (c-a)
// >0: c在ab左侧(逆时针); <0: c在ab右侧(顺时针); =0: 三点共线
double cross(P a, P b, P c) {
return (b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x);
}
// 全局基准点,用于排序比较
P p0;
// 极角排序比较函数
bool cmp(P a, P b) {
double cp = cross(p0, a, b);
if (fabs(cp) > EPS) return cp > 0; // 极角小的排前(逆时针顺序)
return distSq(p0, a) < distSq(p0, b); // 极角相同,距离近的排前
}
/*
* Graham扫描法主函数
* 参数:pts (点集,无需有序)
* 返回:凸包顶点集合 (逆时针顺序)
* 注意:输入点数需 >= 3
*/
vector<P> graham(vector<P>& pts) {
int n = pts.size();
if (n < 3) return pts; // 特判
// 1. 寻找基准点 p0 (y最小,x最小)
int k = 0;
for (int i = 1; i < n; i++) {
if (pts[i].y < pts[k].y || (pts[i].y == pts[k].y && pts[i].x < pts[k].x))
k = i;
}
swap(pts[0], pts[k]);
p0 = pts[0];
// 2. 极角排序 (从pts[1]开始)
sort(pts.begin() + 1, pts.end(), cmp);
// 3. 过滤共线点 (同极角只保留距离最远的)
// 技巧:因为cmp中距离近的在前,所以同角度的最后一个就是最远的
vector<P> q;
q.push_back(p0);
for (int i = 1; i < n; i++) {
// 如果不是最后一个点 且 当前点与下一点共线(极角相同),则跳过当前点
while (i < n - 1 && fabs(cross(p0, pts[i], pts[i+1])) < EPS)
i++;
q.push_back(pts[i]);
}
if (q.size() < 3) return q; // 过滤后不足3点
// 4. 栈扫描
vector<P> st;
st.push_back(q[0]);
st.push_back(q[1]);
for (int i = 2; i < q.size(); i++) {
// 核心:当 (次顶->栈顶->新点) 不构成左转(<=0)时,出栈
// st.size()-2 是次顶,st.back() 是栈顶
while (st.size() >= 2 && cross(st[st.size()-2], st.back(), q[i]) <= EPS) {
st.pop_back();
}
st.push_back(q[i]);
}
return st;
}
// ---------------------------------------------------------
// 使用案例 / 测试
int main() {
int n;
// 假设输入:点数n,然后n行x y
// 示例输入:
// 5
// 0 0
// 1 1
// 2 2
// 0 2
// 2 0
if (!(cin >> n)) return 0;
vector<P> points(n);
for(int i=0; i<n; i++) {
cin >> points[i].x >> points[i].y;
}
// 计算凸包
vector<P> hull = graham(points);
// 打印结果 (如果是计算周长,这里遍历求dist即可)
cout << "Convex Hull Points (" << hull.size() << "):" << endl;
for (const auto& p : hull) {
cout << "(" << p.x << ", " << p.y << ")" << endl;
}
// 扩展:求凸包周长
double perimeter = 0;
for (int i = 0; i < hull.size(); i++) {
perimeter += sqrt(distSq(hull[i], hull[(i + 1) % hull.size()]));
}
printf("Perimeter: %.2f\n", perimeter);
return 0;
}
Jarvis算法
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
// 定义点结构体,重载运算符方便计算
struct P {
long long x, y;
// 判等用于循环终止条件
bool operator==(const P& b) const { return x == b.x && y == b.y; }
};
/*
* 辅助函数:叉积 & 距离
* cross(o, a, b): 计算向量 OA 和 OB 的叉积 (x1*y2 - x2*y1)
* 返回值 > 0: OB 在 OA 左侧 (逆时针)
* 返回值 < 0: OB 在 OA 右侧 (顺时针)
* 返回值 = 0: 三点共线
*/
long long cross(P o, P a, P b) {
return (a.x - o.x) * (b.y - o.y) - (a.y - o.y) * (b.x - o.x);
}
// 两点间距离的平方(不开根号避免精度问题)
long long distSq(P a, P b) {
return (a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y);
}
/*
* 算法板子:Jarvis March 求凸包
* 参数: vector<P> pts - 所有散点
* 返回: vector<P> - 凸包顶点序列(按逆时针排列)
* 复杂度: O(NH),N为点数,H为凸包顶点数。最坏O(N^2)。
* 适用: 点数不多(N<=1000) 或 凸包顶点很少的情况。
*/
vector<P> jarvis(vector<P> pts) {
int n = pts.size();
if (n < 3) return pts; // 点少于3个直接返回
vector<P> hull;
// 1. 寻找起始点:最左下角的点 (y最小,x最小)
int l = 0;
for (int i = 1; i < n; i++) {
if (pts[i].y < pts[l].y || (pts[i].y == pts[l].y && pts[i].x < pts[l].x))
l = i;
}
int cur = l;
// 2. 循环寻找下一个点
do {
hull.push_back(pts[cur]);
// 假设下一个点是 (cur + 1) % n
int nxt = (cur + 1) % n;
// 遍历所有点,找最逆时针的点
for (int i = 0; i < n; i++) {
long long val = cross(pts[cur], pts[nxt], pts[i]);
// 如果 i 在 cur->nxt 的左侧 (更逆时针),更新 nxt
// 或者 共线但 i 距离 cur 更远 (跳过中间点,取最远端点)
if (val > 0 || (val == 0 && distSq(pts[cur], pts[i]) > distSq(pts[cur], pts[nxt]))) {
nxt = i;
}
}
cur = nxt; // 移动到下一点
} while (cur != l); // 直到回到起点
return hull;
}
/*
* 功能函数:打印结果
* 参数: 凸包点集
*/
void printHull(const vector<P>& hull) {
cout << "凸包顶点数量: " << hull.size() << endl;
for (const auto& p : hull) {
cout << "(" << p.x << ", " << p.y << ")" << endl;
}
}
// 示例主函数
int main() {
// 测试数据:包含内部点、边界共线点
vector<P> points = {
{0, 3}, {1, 1}, {2, 2}, {4, 4},
{0, 0}, {1, 2}, {3, 1}, {3, 3},
{2, 0} // {2,0} 与 {0,0},{3,1} 可能在凸包边上
};
// 1. 获取凸包
vector<P> res = jarvis(points);
// 2. 打印结果
printHull(res);
return 0;
}
别人的
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
int n;
struct ben
{
double x,y;
}p[maxn],s[maxn];
double check(ben a1,ben a2,ben b1,ben b2)//检查叉积是否大于0,如果是a就逆时针转到b
{
return (a2.x-a1.x)*(b2.y-b1.y)-(b2.x-b1.x)*(a2.y-a1.y);
}
double d(ben p1,ben p2)//两点间距离。。。
{
return sqrt((p2.y-p1.y)*(p2.y-p1.y)+(p2.x-p1.x)*(p2.x-p1.x));
}
bool cmp(ben p1,ben p2)//排序函数,这个函数别写错了,要不然功亏一篑
{
double tmp=check(p[1],p1,p[1],p2);
if(tmp>0)
return 1;
if(tmp==0&&d(p[0],p1)<d(p[0],p2))
return 1;
return 0;
}
int main()
{
scanf("%d",&n);
double mid;
for(int i=1;i<=n;i++)
{
scanf("%lf%lf",&p[i].x,&p[i].y);
if(i!=1&&p[i].y<p[1].y)//这是找最低点
{
mid=p[1].y;p[1].y=p[i].y;p[i].y=mid;
mid=p[1].x;p[1].x=p[i].x;p[i].x=mid;
}
}
sort(p+2,p+1+n,cmp);//系统快排
s[1]=p[1];//最低点一定在凸包里
int cnt=1;
for(int i=2;i<=n;i++)
{
while(cnt>1&&check(s[cnt-1],s[cnt],s[cnt],p[i])<=0) //判断前面的会不会被踢走,如果被踢走那么出栈
cnt--;
cnt++;
s[cnt]=p[i];
}
s[cnt+1]=p[1];//最后一个点回到凸包起点
double ans=0;
for(int i=1;i<=cnt;i++)
ans+=d(s[i],s[i+1]);//然后s里存好了凸包序列,只需要把两两距离累加就行
printf("%.2lf\n",ans);
return 0;
}最近点对
#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>
#include <iomanip>
using namespace std;
// 定义无穷大
const double INF = 1e20;
struct Pt {
double x, y;
};
// 1. 辅助函数:计算两点欧几里得距离
// 参数:两个点 a, b
// 返回:double 类型的距离
double dis(const Pt& a, const Pt& b) {
return sqrt(pow(a.x - b.x, 2) + pow(a.y - b.y, 2));
}
// 2. 辅助函数:按 x 坐标排序的比较器
bool cmpx(const Pt& a, const Pt& b) {
return a.x < b.x;
}
// 3. 辅助函数:按 y 坐标排序的比较器 (用于分治合并阶段)
bool cmpy(const Pt& a, const Pt& b) {
return a.y < b.y;
}
// 全局数组,方便操作
vector<Pt> p;
// ================== 核心算法板子 ==================
// 参数:当前处理的区间下标 [l, r]
// 返回:该区间内的最近点对距离
// 复杂度:O(N log^2 N)
double solve(int l, int r) {
// 边界处理:如果区间内点很少,直接暴力计算
// 这里的常数可以取大一点,比如 20,减少递归层数
if (r - l <= 3) {
double min_d = INF;
for (int i = l; i <= r; ++i) {
for (int j = i + 1; j <= r; ++j) {
min_d = min(min_d, dis(p[i], p[j]));
}
}
return min_d;
}
// 1. 分治
int mid = (l + r) / 2;
double mid_x = p[mid].x; // 记录中间线的x坐标
double d = min(solve(l, mid), solve(mid + 1, r));
// 2. 合并 (处理跨越左右两边的点)
// 收集所有在中间带状区域内的点 (x距离 mid_x 小于 d)
vector<Pt> tmp;
for (int i = l; i <= r; ++i) {
if (abs(p[i].x - mid_x) < d) {
tmp.push_back(p[i]);
}
}
// 3. 按 y 坐标排序带状区域内的点
sort(tmp.begin(), tmp.end(), cmpy);
// 4. 线性扫描更新 d
// 核心优化:内层循环只需要检查 y 坐标差值小于 d 的点
// 理论上最多只需要检查 6~8 个点,所以这一步是线性的
for (int i = 0; i < tmp.size(); ++i) {
for (int j = i + 1; j < tmp.size(); ++j) {
// 如果 y 差值已经超过 d,后面的肯定更远,直接 break
if (tmp[j].y - tmp[i].y >= d) break;
d = min(d, dis(tmp[i], tmp[j]));
}
}
return d;
}
// ==================================================
int main() {
// 优化 I/O
ios::sync_with_stdio(0); cin.tie(0);
int n;
// 使用案例:输入 n 个点
if (cin >> n) {
p.resize(n);
for (int i = 0; i < n; ++i) {
cin >> p[i].x >> p[i].y;
}
// 重要预处理:先按 x 坐标排序
sort(p.begin(), p.end(), cmpx);
// 调用模板
double ans = solve(0, n - 1);
// 输出结果,通常保留几位小数
cout << fixed << setprecision(4) << ans << endl;
}
return 0;
}九、FFT
手写复数
struct Complex {
double x, y; // 实部和虚部
// 构造函数
Complex(double x = 0, double y = 0) : x(x), y(y) {}
// 运算符重载(关键优化点)
// 使用 const引用 传参,或者直接传值(对于两个double,传值甚至更快)
Complex operator + (const Complex& b) const {
return Complex(x + b.x, y + b.y);
}
Complex operator - (const Complex& b) const {
return Complex(x - b.x, y - b.y);
}
// 复数乘法:(a+bi)(c+di) = (ac - bd) + (ad + bc)i
Complex operator * (const Complex& b) const {
return Complex(x * b.x - y * b.y, x * b.y + y * b.x);
}
};
// 几个辅助函数,为了兼容 std::complex 的写法,不用改太多代码
inline double real(const Complex& a) { return a.x; }
inline double imag(const Complex& a) { return a.y; }
// 构造共轭复数(有些优化版本会用到)
inline Complex conj(const Complex& a) { return Complex(a.x, -a.y); }DFT
// ==================== 朴素 DFT 模板(可打印) ====================
#include <bits/stdc++.h>
using namespace std;
// 复数类型别名
using cd = complex<double>;
// 圆周率
const double PI = acos(-1.0);
/*
* 函数名:dft
* 功能:对序列做离散傅里叶变换(DFT)或逆变换(IDFT)
*
* 数学上:
* 正变换(invert = false):
* y[k] = sum_{j=0}^{n-1} a[j] * exp( 2πi * j*k / n )
* 逆变换(invert = true):
* a[j] = (1/n) * sum_{k=0}^{n-1} y[k] * exp( -2πi * j*k / n )
*
* 参数:
* a —— 输入序列,长度为 n 的复数向量
* invert —— false 表示做正变换(DFT),true 表示做逆变换(IDFT)
*
* 返回值:
* 一个长度同样为 n 的复数向量,表示变换后的结果
*
* 复杂度:
* O(n^2),适合 n 比较小(比如几千以内),或者做对拍。
*/
vector<cd> dft(const vector<cd> &a, bool invert) {
int n = (int)a.size();
vector<cd> res(n);
for (int k = 0; k < n; ++k) {
cd sum(0.0, 0.0); // 累加结果
for (int j = 0; j < n; ++j) {
// 角度 = 2π * j * k / n
// invert = false(正变换):用 + 号
// invert = true (逆变换):用 - 号,并最后除以 n
double angle = 2 * PI * j * k / n * (invert ? 1.0 : -1.0);
cd w(cos(angle), sin(angle)); // e^{i * angle}
sum += a[j] * w;
}
if (invert) sum /= n; // 逆变换要除以 n
res[k] = sum;
}
return res;
}
/*
*(可选)对实数序列的 DFT 封装:
* 输入一个 double 数组,自动转换成复数做 DFT
*/
vector<cd> dft_real(const vector<double> &a, bool invert) {
vector<cd> tmp(a.size());
for (size_t i = 0; i < a.size(); ++i) tmp[i] = cd(a[i], 0.0);
return dft(tmp, invert);
}
//-------------------- 使用示例(需要的话可以自己删 main) --------------------//
int main() {
// 示例:对长度为 4 的实数序列做 DFT 和逆 DFT
vector<double> real_a = {1.0, 0.0, 2.0, 1.0};
// 做正变换(频域)
vector<cd> y = dft_real(real_a, false);
cout << "DFT result (real, imag):\n";
for (int k = 0; k < (int)y.size(); ++k) {
cout << "k = " << k << " : "
<< y[k].real() << " , " << y[k].imag() << "\n";
}
// 做逆变换(回到时域)
vector<cd> back = dft(y, true);
cout << "\nInverse DFT result (should be close to original):\n";
for (int j = 0; j < (int)back.size(); ++j) {
cout << "j = " << j << " : "
<< back[j].real() << " , " << back[j].imag() << "\n";
}
return 0;
}FFT-多项式相乘
#include <iostream>
#include <cmath>
#include <algorithm>
#include <vector>
using namespace std;
const double PI = acos(-1.0);
const int MAXN = 262144 + 5; // 2^18,根据题目要求修改
// === 1. 手写 Complex ===
struct Complex {
double x, y;
Complex(double x = 0, double y = 0) : x(x), y(y) {}
Complex operator+(const Complex &b) const { return Complex(x + b.x, y + b.y); }
Complex operator-(const Complex &b) const { return Complex(x - b.x, y - b.y); }
Complex operator*(const Complex &b) const { return Complex(x * b.x - y * b.y, x * b.y + y * b.x); }
};
// === 2. 封装后的 FFT 函数 ===
// a: 复数数组
// n: 变换长度 (必须是 2 的幂)
// type: 1 为 DFT, -1 为 IDFT
void fft(Complex *a, int n, int type) {
// 使用 static 变量,只有当 n 发生变化时才重新计算 rev
// 这样 A 和 B 做 FFT 时,如果长度一样,第二次调用不会有额外开销
static int rev[MAXN];
static int last_n = 0;
if (n != last_n) {
last_n = n;
int bit = 0;
// 计算 n 对应的二进制位数 (例如 n=8, bit=3)
while ((1 << bit) < n) bit++;
// 重新计算 rev 数组
for (int i = 0; i < n; i++) {
rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));
}
}
// 1. 根据 rev 数组进行位逆序置换 (Swap)
for (int i = 0; i < n; i++) {
if (i < rev[i]) swap(a[i], a[rev[i]]);
}
// 2. 蝴蝶变换 (标准流程)
for (int mid = 1; mid < n; mid <<= 1) {
Complex Wn(cos(PI / mid), type * sin(PI / mid));
for (int R = mid << 1, j = 0; j < n; j += R) {
Complex w(1, 0);
for (int k = 0; k < mid; k++, w = w * Wn) {
Complex x = a[j + k];
Complex y = w * a[j + k + mid];
a[j + k] = x + y;
a[j + k + mid] = x - y;
}
}
}
// 3. IDFT 最后除以 n
if (type == -1) {
for (int i = 0; i < n; i++) a[i].x /= n;
}
}
// === 使用示例 ===
Complex a[MAXN], b[MAXN];
int main() {
int n, m;
cin >> n >> m; // 输入 A 和 B 的次数
// 读入系数
for (int i = 0; i <= n; i++) cin >> a[i].x;
for (int i = 0; i <= m; i++) cin >> b[i].x;
// 计算 limit (2 的幂次)
int limit = 1;
while (limit <= n + m) limit <<= 1;
fft(a, limit, 1); // DFT A
fft(b, limit, 1); // DFT B
// 点乘
for (int i = 0; i < limit; i++) a[i] = a[i] * b[i];
// IDFT
fft(a, limit, -1);
// 输出
for (int i = 0; i <= n + m; i++)
printf("%d ", (int)(a[i].x + 0.5));
return 0;
}
大数相乘
#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>
#include <string>
using namespace std;
const double PI = acos(-1.0);
// 这里的 MAXN 要开到 len(A) + len(B) 的下一级 2 的幂
// 比如两个 10万位的数相乘,结果是 20万位,limit 会是 262144,为了保险开大一点
const int MAXN = 400005;
// === 1. 复数结构体 ===
struct Complex {
double x, y;
Complex(double x = 0, double y = 0) : x(x), y(y) {}
Complex operator+(const Complex &b) const { return Complex(x + b.x, y + b.y); }
Complex operator-(const Complex &b) const { return Complex(x - b.x, y - b.y); }
Complex operator*(const Complex &b) const { return Complex(x * b.x - y * b.y, x * b.y + y * b.x); }
};
// === 2. 封装好的 FFT 函数 (不做修改) ===
void fft(Complex *a, int n, int type) {
static int rev[MAXN];
static int last_n = 0;
if (n != last_n) {
last_n = n;
int bit = 0;
while ((1 << bit) < n) bit++;
for (int i = 0; i < n; i++) {
rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));
}
}
for (int i = 0; i < n; i++) {
if (i < rev[i]) swap(a[i], a[rev[i]]);
}
for (int mid = 1; mid < n; mid <<= 1) {
Complex Wn(cos(PI / mid), type * sin(PI / mid));
for (int R = mid << 1, j = 0; j < n; j += R) {
Complex w(1, 0);
for (int k = 0; k < mid; k++, w = w * Wn) {
Complex x = a[j + k];
Complex y = w * a[j + k + mid];
a[j + k] = x + y;
a[j + k + mid] = x - y;
}
}
}
if (type == -1) {
for (int i = 0; i < n; i++) a[i].x /= n;
}
}
// 存放系数的数组,定义在全局防止爆栈
Complex a[MAXN], b[MAXN];
// 存放最终进位处理后的整数结果
int ans[MAXN];
int main() {
// 优化输入输出
ios::sync_with_stdio(false);
cin.tie(0);
string s1, s2;
cin >> s1 >> s2;
int n = s1.length();
int m = s2.length();
// === 步骤 1: 字符串转多项式系数 ===
// 注意:大数乘法要倒序存储,个位放在索引 0
// 例如 "123" -> a[0]=3, a[1]=2, a[2]=1
// 记得初始化清空,因为全局数组虽然默认0,但多组数据时需要注意
for(int i = 0; i < MAXN; i++) a[i] = b[i] = Complex(0, 0);
for (int i = 0; i < n; i++) a[i].x = s1[n - 1 - i] - '0';
for (int i = 0; i < m; i++) b[i].x = s2[m - 1 - i] - '0';
// === 步骤 2: 确定 FFT 长度 limit ===
int limit = 1;
while (limit < n + m) limit <<= 1;
// === 步骤 3: FFT 计算卷积 ===
fft(a, limit, 1); // DFT
fft(b, limit, 1); // DFT
// 点值相乘
for (int i = 0; i < limit; i++) a[i] = a[i] * b[i];
fft(a, limit, -1); // IDFT
// === 步骤 4: 处理进位 ===
// FFT 的结果是浮点数,先四舍五入转 int
// 卷积后的每一位可能会超过 10,比如算出 58,就要保留 8,进位 5
for (int i = 0; i < limit; i++) {
ans[i] = (int)(a[i].x + 0.5);
}
for (int i = 0; i < limit; i++) {
if (ans[i] >= 10) {
ans[i + 1] += ans[i] / 10;
ans[i] %= 10;
}
}
// === 步骤 5: 输出结果 ===
// 寻找最高位的非零数字(去除前导零)
// 结果长度最多是 n + m,所以从 limit 开始往下找即可
int len = limit;
while (len > 0 && ans[len] == 0) len--;
// 倒序输出(因为我们存的时候是倒着存的,高位在后面)
for (int i = len; i >= 0; i--) {
cout << ans[i];
}
cout << endl;
return 0;
}
十、字符串
KMP
#include <bits/stdc++.h>
const int maxn = 1e5;
using namespace std;
int ne[maxn];
char pattern[maxn],text[maxn];
void GetNext(char p[],int nex[],int n)
{
nex[0] = -1;
int k = -1;
int j = 0;
while (j < n - 1)
{
//p[k]表示前缀,p[j]表示后缀
if (k == -1 || p[j] == p[k])
{
++k;
++j;
nex[j] = k;
}
else
{
k = nex[k];
}
}
}
int KmpSearch(int m,int n)
{
GetNext(pattern,ne,n);
int pLen = n;
int sLen = m;
int i = 0;
int j = 0;
while(i<sLen){
if(j==n-1&&text[i]==pattern[j]){
printf("found the number %d\n",i-j);
}
if(text[i]==pattern[j]){
i++;
j++;
}
else{
j = ne[j];
if(j==-1){
i++;
j++;
}
}
}
}
int main(){
char t[] = "qwqwqwABABCABAAqABABCABAA";
char p[]= "ABABCABAA";
for(int i=0;i<100;i++){
pattern[i] = p[i];
text[i] = t[i];
}
KmpSearch(40,9);
return 0;
}有限状态机FA
#include <iostream>
#include <vector>
#include <string>
#include <cstring>
using namespace std;
// 定义字符集大小,这里假设是 ASCII 码
#define NO_OF_CHARS 256
/**
* @brief 计算当处于状态 state,且遇到字符 x 时,下一个状态应该是多少
*
* @param pat 模式串
* @param M 模式串长度
* @param state 当前状态 (0 到 M)
* @param x 输入的字符
* @return int 下一个状态
*/
int getNextState(const string& pat, int M, int state, int x) {
// 情况 1: 如果字符 x 刚好是模式串中下一个想要匹配的字符
// 这里的 state < M 保证没有越界,pat[state] 就是第 state+1 个字符(索引从0开始)
if (state < M && x == pat[state]) {
return state + 1;
}
// 情况 2: 字符不匹配,或者已经到了结束状态。
// 我们需要找到一个最大的 k,使得:
// pat[0...k-1] 是 (pat[0...state-1] + x) 的后缀
// ns 表示 next_state,我们尝试从最长的可能长度开始递减尝试
// 最长的可能长度就是 state(因为加了一个 x 但匹配失败了,通常长度不会超过当前)
// 实际上,如果 state=5, 遇到错字符,最长也就可能是 5 (比如 AAAAA 遇到 A)
for (int ns = state; ns > 0; ns--) {
// 检查 pat[ns-1] 是否等于 x
if (pat[ns - 1] == x) {
// 如果最后一个字符匹配,我们需要检查前面的 ns-1 个字符是否也匹配
// 即:检查 pat[0...ns-2] 是否等于 pat[state-(ns-1)...state-1]
int i;
for (i = 0; i < ns - 1; i++) {
// pat[i] 是前缀的第 i 个
// pat[state - (ns - 1) + i] 是当前已匹配串的对应后缀位置
if (pat[i] != pat[state - (ns - 1) + i])
break;
}
// 如果循环完整走完,说明完全匹配
if (i == ns - 1)
return ns;
}
}
// 如果找不到任何匹配的前缀,回到状态 0
return 0;
}
/**
* @brief 构建状态转移表 (Transition Function)
*
* @param pat 模式串
* @param TF 二维数组,用于存储结果
*/
void computeTF(const string& pat, int M, int TF[][NO_OF_CHARS]) {
int state, x;
// 遍历每一个可能的状态 (0 到 M)
for (state = 0; state <= M; ++state) {
// 遍历每一个可能的输入字符
for (x = 0; x < NO_OF_CHARS; ++x) {
// 计算跳转
TF[state][x] = getNextState(pat, M, state, x);
}
}
}
/**
* @brief 执行有限自动机字符串匹配
*
* @param pat 模式串
* @param txt 文本串
*/
void search(const string& pat, const string& txt) {
int M = pat.length();
int N = txt.length();
// 1. 创建并计算状态转移表
// 使用 vector 或动态分配防止栈溢出,但在演示中为了清晰使用静态大小或 vector
// 这里使用 vector of vectors 来模拟二维数组,更安全
vector<vector<int>> TF(M + 1, vector<int>(NO_OF_CHARS));
// 为了兼容上面的 computeTF 函数签名(它接受原生数组),这里稍微做个适配
// 或者直接重写 computeTF 使用 vector。为了代码演示最基础的原理,
// 我们这里用原生数组的方式(注意:如果 M 很大,这需要在堆上分配)
// 动态分配二维数组
int (*tf_array)[NO_OF_CHARS] = new int[M + 1][NO_OF_CHARS];
computeTF(pat, M, tf_array);
// 2. 开始匹配过程
int i, state = 0;
for (i = 0; i < N; i++) {
// 核心:根据当前状态和文本字符,直接查表得到新状态
// (unsigned char) 转换是为了防止中文等负数索引越界
state = tf_array[state][(unsigned char)txt[i]];
// 如果状态达到了 M,说明找到了模式串
if (state == M) {
cout << "Pattern found at index " << i - M + 1 << endl;
}
}
delete[] tf_array; // 清理内存
}
int main() {
string txt = "AABAACAADAABAABA";
string pat = "AABA";
cout << "Text: " << txt << endl;
cout << "Pattern: " << pat << endl;
search(pat, txt);
return 0;
}十一、其它常用算法(包括上机中算法)
手写堆
C语言需要自己写一个swap。
如何手写一个堆?
- 插入一个数
heap[++size]; up(size); - 求这个集合之中的最小值
heap[1] - 删除最小值
heap[1] = heap[size]; size--; down(1); - 删除任何一个元素
heap[k] = heap[size]; size--; down(k); up(k); - 修改任何一个元素
heap[k] = x; down(x); up(x);
定义:堆是一个完全二叉树。小根堆递归定义:每个节点小于等于左右儿子,即根节点就是最小值。
存储:假设根节点是$1$,则x的左儿子是$2x$,x的右儿子是$2x+1$。
堆排序:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int n, m;
int h[N], size;
void down(int u){
int t = u;
if(u*2<=size && h[u*2]<h[t]) t = u*2;
if(u*2+1<=size && h[u*2+1]<h[t]) t = u*2+1;
if(u!=t){
swap(h[u],h[t]);
down(t);
}
}
void up(int u){
while(u/2 && h[u/2] < h[u]){
swap(u/2,u);
u >>= 1;
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i = 1; i <= n; i++) scanf("%d", &h[i]);
size = n;
for(int i = n/2; i; i--) down(i); //建堆,不需要down最后一层
while(m--){
printf("%d",&h[1]);
h[1] = h[size];
size--;
down(1);
}
return 0;
}并查集
并查集支持以下操作且可以近乎$O(1)$快速完成以下操作:1️⃣将两个集合合并;2️⃣询问两个元素是否在一个集合当中。
基本原理:使用树维护集合,每棵树是一个集合,每一个集合有一个元素作为根节点,树根的编号就是整个集合的编号,每一个节点存储一个它的父节点,p[x]表示x的父节点。根节点p[x]=x即集合编号。
问题一:如何判断树根,父节点指向自己:if(p[x]==x)
问题二:如何求x的集合编号,通过记录的父节点一直往上找:while(p[x] != x) x = p[x];
问题三:如何合并两个集合:假设p[x]的x的集合编号,p[y]是y的集合编号,直接p[x] = y即可。
问题四:问题二的时间复杂度比较高,可以进行路径优化:查找x的根节点的时候,可以把x和所有路径上的节点都直接指向根节点,优化下一次查找的时间复杂度。
示例:
#include <iostream>
using namespace std;
const int N = 100010;
int n;
int p[N];//记录每个元素的父节点是谁
int find(int x){ //带路径压缩优化,使用递归调用
if(p[x]!=x) p[x] = find(p[x]);
return p[x];
}
int main(){
scanf("%d%d",&n,&m);
for(int i = 1; i <=n ; i++) p[i] = i; //最开始每个元素在一个集合
while(m--){
char op[2];
int a,b;
scanf("%s%d%d",op,&a,&b);
if(op[0]=='M') p[find(a)] = find(b);
else{
if(find(a) == find(b)) puts("Yes");
else puts("No");
}
}
return 0;
}Trie树
用来快速存储和查找字符串集合的数据结构,
每个节点一个字符,每个位置标记是否为结尾。这里使用数组存储Trie树,每一个位置是一个节点,使用son数组记录每个节点的子节点位置。
示例题目:
#include <iostream>
using namespace std;
const int N = 100010;
int n;
int son[N][26], cnt[N] , idx;
//idx代表目前数组开到哪里,下标为0的为空节点。
//son数组记录的是下标为n的节点的子节点。
//cnt记录某个字符串结尾的次数,初始是0。
char str[N];
void insert(char str[]){
int p = 0;
for(int i = 0; str[i]; i++){
int u = str[i] - 'a';
if(!son[p][u]) son[p][u] = ++idx;
p = son[p][u];
}
cnt[p] ++;
}
int query(char str[]){
int p = 0;
for(int i = 0; str[i]; i++){
int u = str[i] - 'a';
if(!son[p][u]) return 0;
p = son[p][u];
}
return cnt[p];
}
int main(){
int n;
scanf("%d",&n);
while(n--){
char op[2];//读成字符串避免scanf读字符出现空格回车
scanf("%s%s",op,str);
if(op[0]=='I') insert(str);
else query(str);
}
return 0;
}KMP
定义KMP数组next[i] = j,即以i为终点的一段的数组里,前面j个元素和最后面j个元素是一样的。
匹配的时候,当匹配到key数组的第k位时,使用next[k]判断这一段数组有多少是相同的,把key数组向后移动strlen(key) - next[k]位,得到新的验证数组位置,就是把验证数组指针指向next[k],而指向匹配数组的指针只用每个循环加1。
#include <iostream>
using namespace std;
const int N = 100010, M = 100010;
int n,m;
int p[N], s[M];
int nxt[N];
int main(){
cin >> n >> p+1 >> m >> s+1;
//求next的过程
for(int i = 2, j = 0; i <= n;i++){
while(j && p[i]!=p[j+1]) j = nxt[j];
if(p[i] == p[j+1]) j++;
nxt[i] = j;
}
//KMP匹配算法
for(int i = 1, j = 0; i<=m; i++){
while (j && s[i]!=p[j+1]) j = nxt[j]; //匹配不上使用next[j]计算前后缀重复区间大小,一直位移到可以匹配上。
if(s[i] == p[j+1]) j++;
if(j==n){
//匹配成功!
}
}
}单调栈
给定一个序列,求一个序列当中每个数左边离他最近的且比他小的数在什么地方。
#include <iostream>
using namespace std;
const int N = 100010;
int n;
int stk[N], tt;
int main(){
cin >> n;
for(int i = 0; i < n; i++){
int x;
cin >> x;
while(tt && stk[tt] >= x) tt --;
if(tt) cout << stk[tt] << endl;
else cout << -1 << ' ';
stk[++tt] = x;
}
return 0;
}区间合并
给定n个区间 $[l_i, r_i]$ ,要求合并所有有交集的区间。
步骤:
- 按区间左端点排序。
- 按左端点从小到大顺序遍历,记录一个当前的区间,扫描接下来的区间是否与当前区间有交集,若有交集则合并在一起并继续扫描,如果没有交集就把当前区间更新为这个区间。
void merge(vector<PII> &segs){
vector<PII> res;
sort(segs.begin(), segs.end());
int st = -2e9, ed = -2e9;
for(auto seg: segs){
if(ed < seg.first){
if (st != -2e9) res.push_back({st,ed});
st = seg.first, ed = seg.second;
}
else ed = max(ed,seg.second);
}
if(st != -2e9) res.push_back({st,ed});
segs = res;
}高精度加减乘除
vector<int> add(vector<int> &A, vector<int> &B){
if (A.size() < B.size()) return add(B, A);
vector<int> C;
int t = 0;
for (int i = 0; i < A.size(); i ++ ){
t += A[i];
if (i < B.size()) t += B[i];
C.push_back(t % 10);
t /= 10;
}
if (t) C.push_back(t);
return C;
}
vector<int> sub(vector<int> &A, vector<int> &B){
vector<int> C;
for (int i = 0, t = 0; i < A.size(); i ++ ){
t = A[i] - t;
if (i < B.size()) t -= B[i];
C.push_back((t + 10) % 10);
if (t < 0) t = 1;
else t = 0;
}
removeZero(C);
return C;
}
vector<int> mul(vector<int> &A, vector<int> &B) {
vector<int> C(A.size() + B.size() + 7, 0); // 初始化为 0
for (int i = 0; i < A.size(); i++)
for (int j = 0; j < B.size(); j++)
C[i + j] += A[i] * B[j];
int t = 0;
for (int i = 0; i < C.size(); i++) {
t += C[i];
C[i] = t % 10;
t /= 10;
}
removeZero(C);
return C;
}
vector<int> div(vector<int> &A, int b, int &r){
vector<int> C;
r = 0;
for (int i = A.size() - 1; i >= 0; i -- )
{
r = r * 10 + A[i];
C.push_back(r / b);
r %= b;
}
reverse(C.begin(), C.end());
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}