软院大二上的算法课真是离谱，课上PPT几乎全是英文（怀疑完全是从算法导论原版书粘贴的），也听不懂。上机考试和上课讲的内容也没有关系，被纯纯虐杀，有的算法听都没听过...

第二章 算法基础

2.1 插入排序

基本算法：

​ 当选择循环下标j时，数组的A[1, j-1]已经排好序，剩余子数组为A[j+1, n]，将j下标的元素插入到前j-1个元素之中的合适位置：查找对应位置需要从j-1到1一个一个找到第一个小于等于A[j]的元素，找过的元素都往后移一位，A[j]放在停止的位置上。而循环下一次下标为j+1。

而当证明算法的正确性时，书中给出了需要证明的三条性质：

• 初始化： 循环的第一次迭代之前，它为真；
• 保持： 如果循环的某次迭代之前它为真，那么下次迭代之前它仍然为真；
• 终止： 在循环终止时，不变是为我们提供了一个有用的性质，该性质有助于证明算法是正确的。

下面用插入算法举例，证明插入算法的正确性：

• 初始化： 当第一次迭代之前（插入算法从j = 2开始循环），子数组仅有单个元素A[1]组成，一个元素当然是已经排好序的了，那么为真；
• 保持： 每次插入元素时，从j-1到1循环，把大于A[j]的元素往后移一位，直到找到A[j]的合适位置（记为k），那么将A[j]的值插入该元素，那么从[1,k-1]和[k+1,j-1]均为排好序的，A[j]大于等于左边，小于右边，总体也是排好的，所以也为真；
• 终止： 循环终止的条件为j > A.length，子数组A[1..n]由原来的A[1..n]组成，但是是排好序的。所以算法正确。

2.2 分析算法

这本书里面使用随机访问机（RAM）模型来计算算法的使用代价。设定其只能执行基本的算数运算、数据移动、控制指令，且指令没有并发操作。

算法分析要看运行时间和输入规模。输入规模可以指输入的项数，也可能是输入总位数、输入本身；运行时间指执行的基本操作数或者步数。

所以分析代码时，可以设定第i行代码执行所需时间为c_i，同时模拟计算得出执行次数和输入规模n之间的关联，对所有行求和可以得到总运行时间 T(n) 的表达式。算法运行时间也和同规模下的不同输入有关系，比如排序数组已经是排好序的，那么就插入算法省去了查找合适位置的过程，此时是最好情况，T(n)是一次线性的；同时也可能是反序排序的，那么需要每个数比较一次，此时是最坏情况，T(n)是二次函数。

我们需要关注算法的增长量级，而可以忽略那些乘上的常数和低阶项。比如插入排序的最坏情况运行时间为$\Theta(n^2)$。

2.3 设计算法

这里讲了分治算法，分治算法在本质是递归的，每层递归有三个步骤：

• 分解原问题为子问题，降低规模；
• 递归地解决这些子问题；
• 合并这些问题的解为原问题的解。

下面用了分治排序为例。分治算法可以写两个函数来实现，分别是MERGE-SORT和MERGE，具体不在阐述了。

分析分治算法等递归的算法时，算法函数包含对自己的调用，可以用递归方程或者递归式来描述其运行时间，然后使用数学公式求解递归方程，得出算法的性能的界。

下面给出分治算法的分析方法，按照上面的递归步骤：假设 T(n) 是规模为 n 的一个问题的运行时间。若问题规模足够小，如对某个常量 c ，$ n \leq c$ ，则直接求解需要常量时间，我们将其写作 $\Theta(1) $。假设把原问题分解成 a 个子问题，每个子问题的规模是原问题的 $ 1/b$ 。为了解决一个规模为 $n/b$ 的子问题，需要 $ T(n/b)$ 的时间，所以需要 $aT(n/b)$ 的时间来求解 a 个子问题。如果分解问题成子问题需要时间 $D(n)$ ，合并子问题的解成原问题的解需要时间 $C(n) $，那么得到递归式：

第三章 函数的增长

3.1 渐近符号

$\Theta$记号：用来表示算法的运行时间，渐进给出一个函数的上界和下界。

就是对于任意情况，都能找到$c_1$和$c_2$使得$f(n)$能夹在两个之间。称$g(n)$是$f(n)$的一个渐进紧确界。

O记号： 只有一个渐进上界，用来反映最坏情况也是总体的最坏运行时间。

$\Omega$记号： 表示渐进下界，表示无论什么输入，程序的最好情况。

o记号： 表示非渐进紧确的上界，即程序的运行时间一定小于某个数量级。

$\omega$记号： 表示非渐进紧确的下界。

3.2 标准记号和常用函数

都是非常常见的数学符号。

记录一下向上取整$\lceil x \rceil$的Latex：\lceil x \rceil 和向下取整$\lfloor x \rfloor$：\lfloor x \rfloor 。

第四章 分支策略

本章讲解了如何求解递归式，得出算法的$\Theta$以及$O$渐进界。总共有以下三种方法：

• 代入法：先猜测一个界，带进去看看是不是对的；
• 递归树法：将递归式转换为一棵树，其结点表示不同层次的递归调用产生的代价；
• 主方法：求解形如$T(n) = aT(n/b) + f(n)$的递归式的界。

4.1 最大子数组问题

给出了这样一个问题：

给你未来17天的一只股票走势图，你可以选择一个点买入，之后的一个点卖出，请问如何使得收益最大化？

如果直接暴力求解，求出所有可能的组合，运行时间会是$\Omega(n^2)$。

书中给的方法是，把这个问题的原始数组（每天的价格）先转换为每天价格变化，那么对应的求解两点之间差最大的问题，就转换为了找到一段连续区间，其中价格变化数组的累加值最大，即代表总差值最大（称这个数组为最大子数组）。

然后就要使用分治法求解这个问题。把数组 A[low..high] 的任意子数组分为三种，最大子数组一定在其中任意一个子问题之中，求出以下三个子问题中的最大和，即为原数组的最大和，即把问题分解：

• 完全处于 A[low..mid] 之中
• 完全处于 A[mid+1..high] 之中
• 跨越中点 mid 的数组

前两个问题和 A[low..high] 没有区别，可以递归求解（当 low = high 时直接return当前元素的值）。而跨越中点的数组需要循环求解：从mid分别往两边循环，记录一个累加值，分别找到两边累加值的最大值，相加即为所求。得出这三个值之后取最大值即为 A[low..high] 的最终结果。

跨越中点的数组求解显然从中间分别向两边循环，运行时间是 $\Theta(n)$ ，从中点拆成两个子问题递归，显然变成两个规模为$1/2$的运行时间。故可得：

其解为 $T(n) = \Theta(n lgn)$ 。

4.2 矩阵乘法的Strassen算法

若 $A=(a_{ij})$ 和 $B = (b_ij)$ 是 $n\times n$ 的方阵，则矩阵乘法 $C = A·B$ 中的元素 $c_{ij}$ 为：

$$ c_{ij} = \sum_{k=1}^{n} a_{ik} \cdot b_{kj} $$

如果直接对于其进行暴力求解，需要嵌套三层循环，时间复杂度是 $\Theta(n)$ 。

此时我们可以思考简单的分治算法，即我们假设n是2的幂次，则每次可以把三个矩阵各自拆分为三个部分，就像：

其中 $ A_{ij} $、$ B_{ij}$ 、$ C_{ij} $都是 $ \frac{n}{2} \times \frac{n}{2}$ 的子矩阵。原本的矩阵乘法 $C = A \cdot B$ ，按照子矩阵块的运算规则，等价于以下4个“子矩阵乘法 + 加法”的公式：

具体完成代码时，我们在递归时可以直接传递下标，避免复制数组元素提升时间复杂度。每次循环相当于把原问题拆解为8个规模为 $n/2$ 的子问题（因为有8个矩阵乘法），同时将最终计算结果复制回原矩阵数组的位置（即合并过程）显然要嵌套两层循环，遍历每个元素，所以总时间为 $\Theta(n^2)$ ，故得到了最终的递归式：

根据计算得出的解仍是 $T(n) = \Theta(n^3)$ ，证明简单的分治方法并不优于前面的直接暴力计算。原因是 $T(n/2)$ 前面的数字8太大了。

而Strassen方法核心思想是只递归进行7次而不是8次 $n/2 \times n/2$ 矩阵的乘法。其本质是矩阵数学的知识，它先把输入的两个矩阵像先前一样，分解为四个子矩阵；然后其创建了10个 $n/2 \times n/2$ 的辅助矩阵，每个矩阵是上面其中两个子矩阵相加或相减的得到的，此处的时间花销是 $\Theta(n^2)$ 量级；然后再递归地算出7个积矩阵，每个矩阵都是上面其中两个辅助矩阵的积，此处是子问题的划分，可以看出只递归出7个子问题；最后通过这7个积矩阵的加减运算，可以得出结果矩阵C的子矩阵，时间花销也是 $\Theta(n^2)$ 量级。

递归式变为：

最终的解为 $T(n) = \Theta(n^{lg7})$ 。

4.3 代入法求解递归式

代入法本质上就是先猜后证。常见步骤：

1. 猜测解的形式
2. 用数学归纳法求出解中的常数，并证明解是正确的

由于渐进符号的定义：

我们不必让所有 $n>0$ 都成立，可以选定一个下界 $n_0$ ，使得大于等于整个数的n都成立即可。

举例：

确定递归式 $T(n) = 2T(\lfloor n/2 \rfloor) + n$ 的上界。

我们猜测其解为 $T(n) = O(n\text{ }lgn)$ 。下面使用归纳法证明：假定这个上界对于所有正整数 $m<n$ 均成立，显然 $m = \lfloor n/2 \rfloor$ 也必然成立，故 $T(\lfloor n/2 \rfloor) \leq c(\lfloor n/2 \rfloor)lg(\lfloor n/2 \rfloor)$ ，代入递归式得到：

如此便得证。

4.4 递归树法求解递归式

递归树是我们把程序的递归画成一棵树的结构。递归树中，每个结点表示一个单一子问题的代价，子问题对应某次递归函数调用。我们将树中每层中的代价求和，得到每层代价，然后将所有层的代价求和，得到所有层次的总代价。

例如：求解递归式 $T(n) = 3T(\lfloor n/4 \rfloor) + \Theta(n^2)$ ：

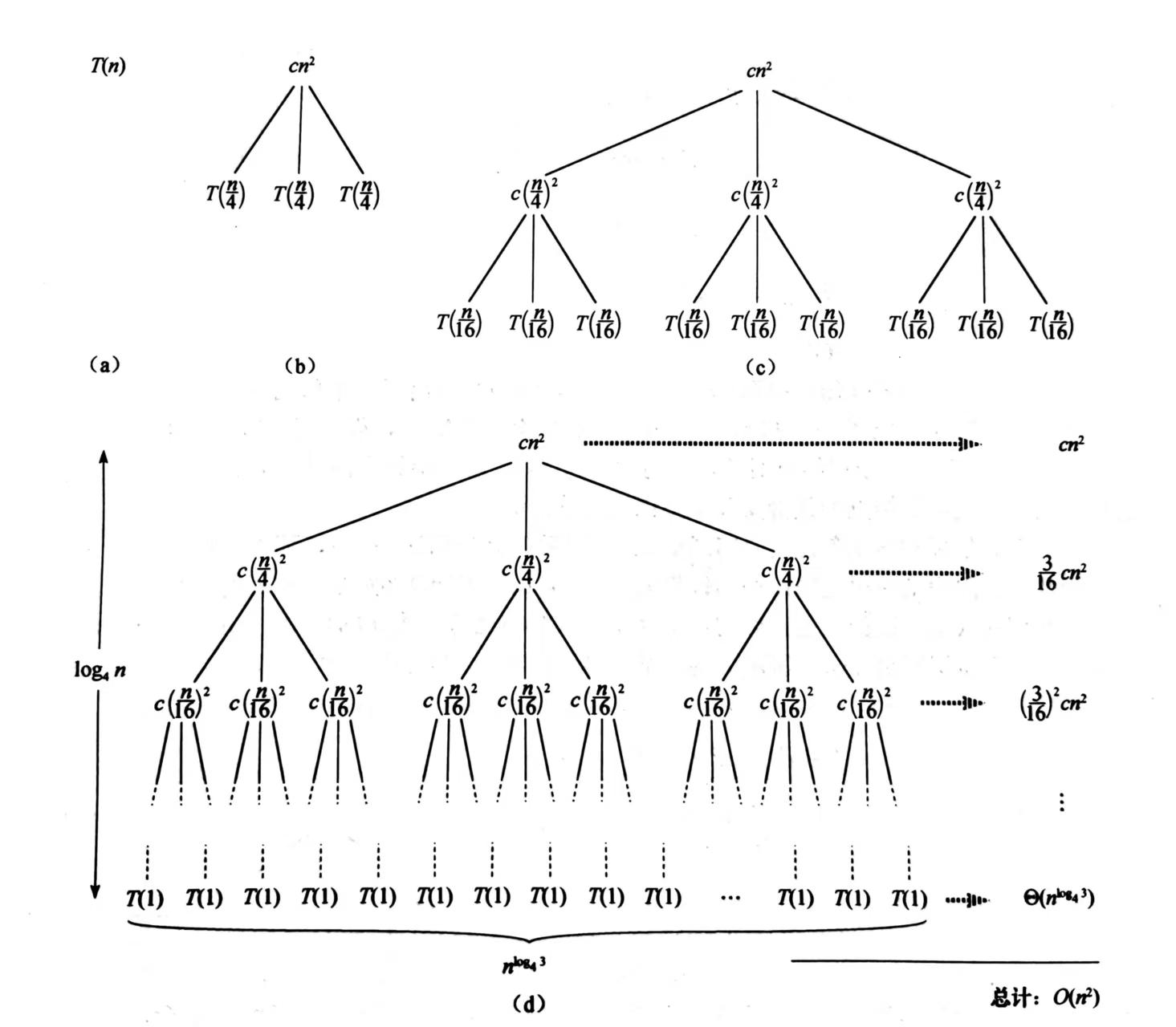
总的代价为：

4.5 主方法求解递归式

主方法可以求解如下形式的递归式：

其中 $a≥1$ 和 $b>1$ 是常数， $f(n)$ 是渐进正函数。

描述的问题是：将规模为n的问题分解为a个子问题，每个子问题的规模为 $n/b$ ，其中 $a$ 和 $b$ 都是正整数。 $a$ 个子问题递归地进行求解，每个花费时间 $ T(n/b)$ 。函数 $f(n)$ 包含问题分解和子问题解合并的代价。

定理 4.1（主定理）

令 $a\geqslant1$ 和 $b>1$ 是常数， $f(n)$ 是一个函数， $T(n)$ 是定义在非负整数上的递归式：

$$ T(n) = aT(n/b) + f(n) $$

其中我们将 $n/b$ 解释为 $\lfloor n/b \rfloor$ 或 $\lceil n/b \rceil$ 。那么 $T(n)$ 有如下渐近界：

1. 若对某个常数 $\varepsilon>0$ 有 $f(n)=O(n^{\log_b a - \varepsilon})$ ，则 $T(n)=\Theta(n^{\log_b a})$ 。
2. 若 $f(n)=\Theta(n^{\log_b a})$ ，则 $T(n)=\Theta(n^{\log_b a} \lg n)$ 。
3. 若对某个常数 $\varepsilon>0$ 有 $f(n)=\Omega(n^{\log_b a + \varepsilon})$ ，且对某个常数 $c<1$ 和所有足够大的 $n$ 有 $af(n/b)\leqslant cf(n)$ ，则 $T(n)=\Theta(f(n))$ 。

使用时我们需要先判断属于三种情况之中的哪一种：将函数 $f(n)$ 与函数 $n^{\log_b a}$ 进行比较（比较的是增长规模，即幂次大小）：

若函数 $n^{\log_b a}$ 更大，如情况 1，则解为 $T(n)=\Theta(n^{\log_b a})$。若函数 $f(n)$ 更大，如情况 3，则解为 $T(n)=\Theta(f(n))$ 。若两个函数大小相当，如情况 2，则乘上一个对数因子，解为 $T(n)=\Theta(n^{\log_b a} \lg n)=\Theta(f(n)\lg n)$ 。

例如计算递归式：

可得 $a = 7$ ， $b = 2$ ，$f(n) = \Theta(n^2)$ ，所以 $n^{\log_b a} = n^{\log_2 7}$ ，所以 $\log_2 7 > 2.80 > 2$ ，所以应用情况1，得出解 $T(n) = \Theta(n^{lg7})$ 。

4.6 证明主定理

bur我闲的没事证他干什么。

第五章 概率分析和随机算法

不太懂这一章何意味。

5.1 雇用问题

书中给了这样一个现实问题：

你是老板，要雇佣一名员工，你只能按顺序面试，面试时雇佣一个员工也要花费一定的费用$c_h$，面试每一个人之后要立即决定是否录用。想在所有的面试者里面选择最好的面试者来录用，即面试到比当前员工更好的面试者时，直接把当前的人开了，雇佣新的员工，当然要重新支付雇佣费用。

最坏情况下，面试者质量按照次序递增，那么需要雇佣$n$次，需要花费$n\times c_h$的费用。

其实这个问题花的价格就相当于代码运行过程中消耗的时间，分析不同分布的数据需要进行概率分析，通过计算随机状态下数据的分布，计算平均情况运行时间。

如果算法不仅由输入决定，也由随机数生成器的数值决定，那么把这样随机算法的运行时间称为期望运行时间。

5.2 指示器随机变量

给定样本空间S和一个事件A，那么事件A对应的指示器随机变量 $I\{A\}$ 定义为：

引理 5.1

给定一个样本空间S和S中的一个事件A，设$X_A = I\{A\}$ ，那么 $E[X_A] = Pr\{A\}$。

所以当我们计算一个变量 $X$ ，比如用 $X$ 表示 $n$ 次抛硬币正面向上的总次数，$X_i$ 表示第 $i$ 次是否投出正面，则可以使用指示器随机变量分析正面出现次数的期望：

对于5.1的雇用问题，使用这个方法研究：设 $X_i$ 表示第 $ i$ 个应聘者被雇用。若第 $ i$ 个人被雇用，证明比前 $i-1$ 个应聘者都优秀，这个的概率为 $1/i$ 。所以：

所以雇佣问题的雇用平均费用为 $O(c_h ln\text{ } n)$。

5.3 随机算法

这一节给了一个生成随机排列数组的方法。

给定一个数组A，包含元素1到n。新建一个优先级数组$P[i]$，对于每个$ i$，取一个 $1 - n^3$ 之间的随机数。把A和P关联起来，然后按照P数组的元素大小排序，最后得到“打乱”的A数组。此时A数组是一个均匀随机排列。

书上后面一直在证明它是均匀随机排列。

第六章 堆排序

6.1 堆

堆是一个二叉树，除了最底层外，树是完全充满的，且最底层从左向右填充。

二叉堆可以用两种形式：最大堆和最小堆。定义为：最大堆指除了根以外所有节点 $i$ 满足 $A[parent(i)] ≥ A[i]$ ，最大元素存在根节点里面。最小堆则相反。

6.2 维护堆的性质

为了维持堆的性质，书里给了一个MAX-HEAPIFY函数，给定数组中一个元素的位置i，i的左右子树都是最大堆，但i可能不满足性质，对i的子树维护堆的性质。

思路就是每次找到节点和两个孩子的最大值，如果最大值等于节点，则结束递归；如果最大值是某个孩子，则节点和这个孩子交换，并且使用这个孩子作为节点继续进行递归。

这里我们可以把书中的“MAX-HEAPIFY”操作称作down操作，形象地说是把i节点向下的部分进行操作，以满足堆的性质；同时堆有时需要把一个元素向上转移（比如把一个新的元素插在最后面），同时可以定义一种up操作。借助这两个函数能完成所有的堆操作。

// 以大顶堆为例
void down(int u){
    int t = u;
    if(u*2<=size && h[u*2]<h[t]) t = u*2;
    if(u*2+1<=size && h[u*2+1]<h[t]) t = u*2+1;
    if(u!=t){
        swap(h[u],h[t]);
        down(t);
    }
}

void up(int u){
    while(u/2 && h[u/2] < h[u]){
        swap(u/2,u);
        u >>= 1;
    }
}

书中计算了down操作的时间复杂度。因为每个子树的大小最多为 $\frac{2}{3}n$ （正好最后一层填充一半），所以可以得出递推式：

利用主定理可以得出这个操作的时间复杂度是 $O(ln\text{ }n)$ 。

根据down和up两个操作可以得出以下操作：（From 第二章 数据结构 - Alex Li的学习笔记）

1. 插入一个数 heap[++size]; up(size);
2. 求这个集合之中的最小值 heap[1]
3. 删除最小值 heap[1] = heap[size]; size--; down(1);
4. 删除任何一个元素 heap[k] = heap[size]; size--; down(k); up(k);
5. 修改任何一个元素 heap[k] = x; down(x); up(x);

6.3 建堆

使用自底而上的方法把一个大小为 $A.length$ 的数组转换为最大堆。因为 $A(n/2 +1..n)$ 的元素都是树的叶节点，所以循环 $i$ 从 $n/2$ 开始下降到 $1$ 即可，每一次执行一次 down(i) 操作。

for(int i = n/2; i; i--) down(i);

总的建堆时间复杂度是 $O(n)$ 。

6.4 堆排序算法

给定数组 $A[n]$ ，

• 先使用上一节的算法建堆，把这个数组建成一个最大堆；
• 然后取出 $A[1]$ ，即为整个数组最大值，放入结果当中；
• 然后进行删除这个元素的操作，即把 $A[1]$ 与 $A[n]$ 互换，然后进行down(1)操作，重新维护堆的性质，再重复步骤二即可。

6.5 优先队列

优先队列是一种用来维护由一组元素构成的集合S的数据结构，其中每一个元素都有一个相关的值，称为关键字。分为最大优先队列和最小优先队列（类比最大堆、最小堆）。一个最大优先队列支持以下操作：

• INSERT(S, x)：把元素 x 插入集合 S 中。这一操作等价于 S = S $\cup$ {x} 。
• MAXIMUM(S)：返回 S 中具有最大关键字的元素。
• EXTRACT-MAX(S)：去掉并返回 S 中的具有最大关键字的元素。
• INCREASE-KEY(S, x, k)：将元素 x 的关键字值增加到 k ，这里假设 k 的值不小于 x 的原关键字值。

可以用堆来实现优先队列，需要在堆中存储对应对象的句柄（用来和对象相对应），取决于具体的元素，一般存储数组的下标。

如何实现？

这里的MAXIMUM(S)可以直接返回堆顶元素；EXTRACT-MAX(S)把1和n元素互换，并对1执行down操作，最后返回原来的堆顶；INCREASE-KEY把某个元素关键字改为k之后，对这个元素执行up操作即可；INSERT操作直接把元素添加到末尾，然后执行一下up操作。

第七章 快速排序

感觉这章后面几节的内容都没什么意义，全在各种分析算法。

（以下内容摘自 第一章 基础算法（一） - Alex Li的学习笔记）

主要思想：分治

1. 确定分界点：q[l]或者q[(l+r)/2]或者q[r]；
2. 调整范围：目标是左边的数都小于等于x，右边的数都大于等于x（分界点不一定是x）；
3. 递归处理左右两端。

第二步的思路：

1. 设定两个指针，从左右两端开始：

   • 左指针从左向右寻找第一个大于等于基准的元素
   • 右指针从右向左寻找第一个小于等于基准的元素
2. 找到之后交换两个元素
3. 持续移动左右指针并交换元素，直到两个指针相遇，此时结束

以下是代码：

void quicksort(int a[], int l, int r){
    if(l>=r) return;
    int cha = a[l];
    int x = l+1, y = r;
    while(x<=y){
        while(x<=y){
            if(a[x]>cha) break;
            x++;
        }
        while(x<=y){
            if(a[y]<cha) break;
            y--;
        }
        if(x<y){
            swap(a[x],a[y]);
        }
    }
    swap(a[l],a[y]);
    if(l<y)quicksort(a,l,y-1);
    if(y+1<r)quicksort(a,y+1,r);
}

书里面还给了一种随机化版本（7.3节），原本是把区间左或右端点作为基准元素，书里面随机取了左端点到右端点的一个元素作为基准元素。

第十五章 动态规划

实在不想看书了。

第五章 动态规划（一） - Alex Li的学习笔记

第五章 动态规划（二） - Alex Li的学习笔记

推荐资源（提取码86ob）：https://www.alipan.com/s/H2A4vEGVd7T?pwd=86ob