本章主要介绍动态规划的常用思路，并介绍了背包问题里面的01背包、多重背包的解题思路和代码

01背包

01背包问题为：给定背包总体积，给N个物品，每个物品有一个体积和重量，只能用一次或不用，问最大重量是多少？
下面是思路，定义函数f(i,j)代表：仅包含前i个物品且总体积小于等于j的背包的最大价值是多少，故最终需要的结果是f(N,V)。
初始时把所有值都设为0，且i或j等于0的本身值就为0。
对于一个新的状态f(i,j)，可能的值有下面两种可能，如果包含i，则答案为f(i-1，j-vi) + wi；如果不包含i，则为f(i-1,j)。这两个值取最大值就可以算出f(i,j)。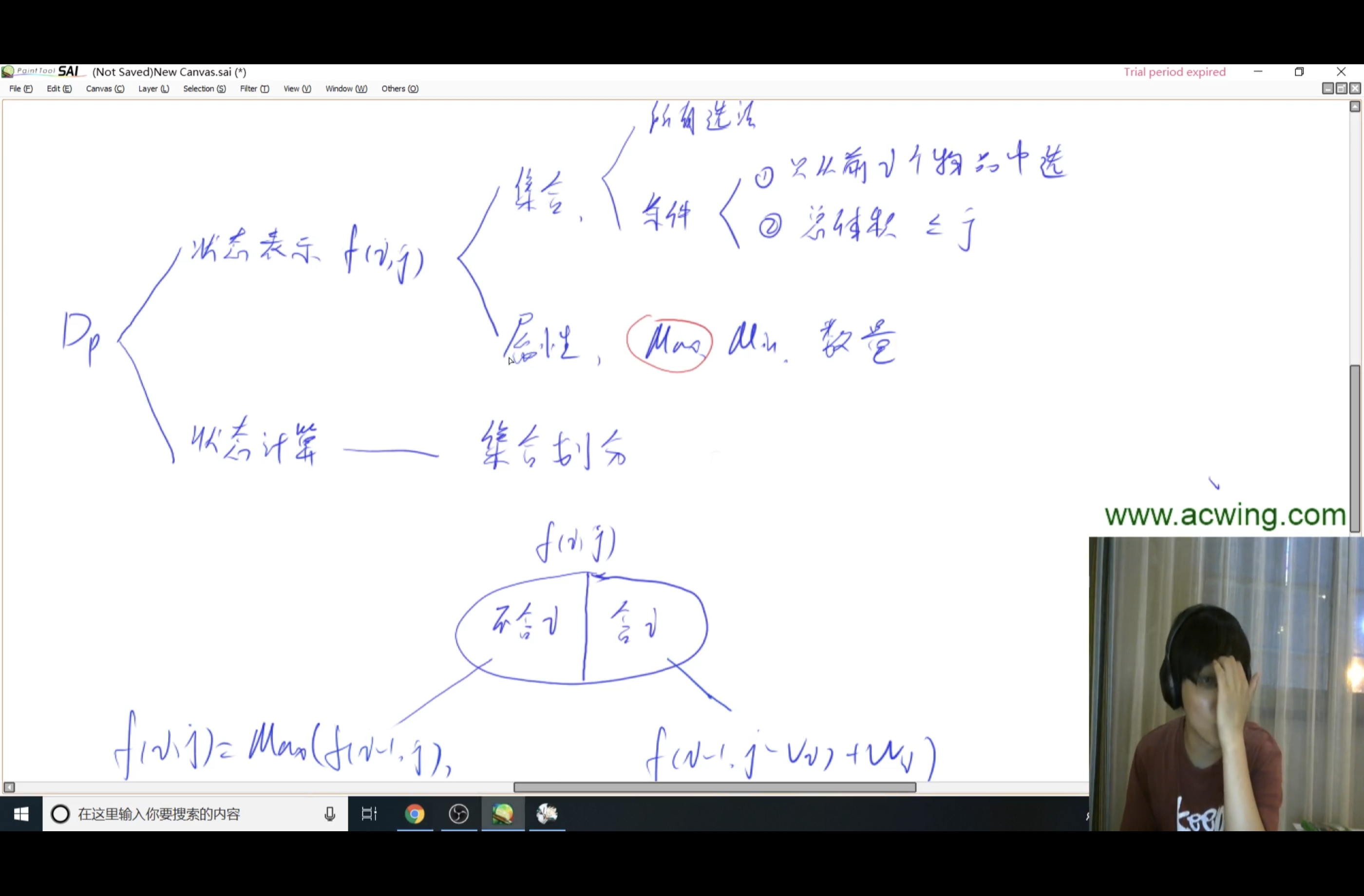

代码：

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N][N];

int main(){
    cin >> n >> m;
    for(int i=1; i <= n; i++) cin >> v[i] >> w[i];
    for(int i=1; i <= n; i++)｛
        for(int j = 1; j <= m; j++){
            f[i][j] = f[i-1][j];
            if(j >= v[i]) f[i][j] = max(f[i][j], f[i-1][j-v[i]] + w[i]);
        }
    ｝
    cout << f[n][m] << endl;
}

完全背包

完全背包的区别是每个物品可以选0-无数次，同样求最大总重量。
思路： 此时DP数组的含义不变。在每次选择f(i,j)时，同样也变成了k+1种选择（选择0,1,2,…,k个第i个元素，k由循环判断当前的j能否大于或等于k个i的价值，即k*wi <= j），循环判断出其中的最大值，就可以算出新的f[i,j]。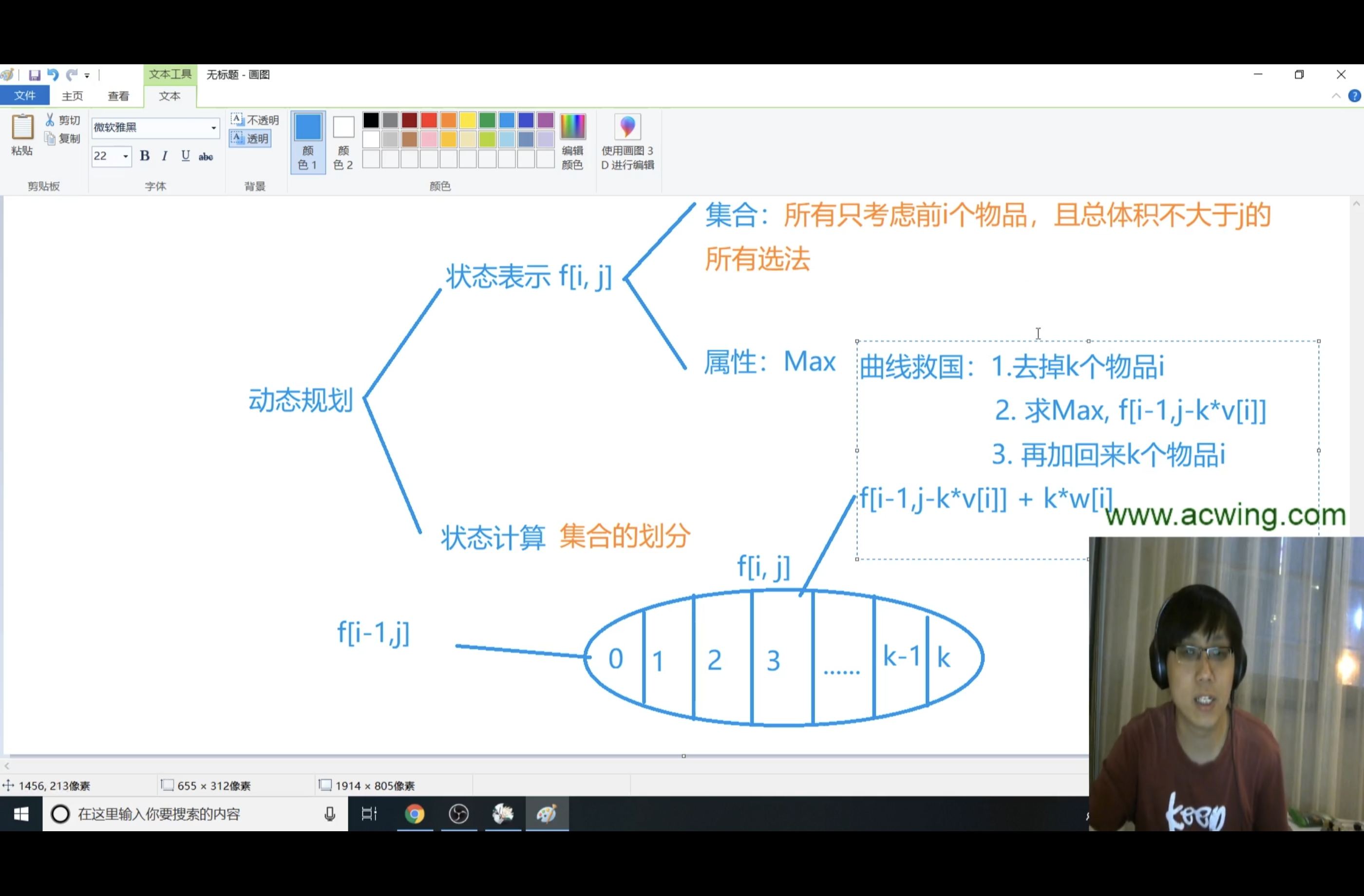

代码：

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];

int main(){
    cin >> n >> m;
    for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
    for(int i = 1; i <= n; i ++){
        for(int j = 0; j <= m; j++){
            for(int k = 0; k*v[i] <= j ; k ++)
                f[i][j] = max(f[i][j], f[i-1][j-v[i]*k + w[i]*k]);
        }
    }
    cout << f[n][m] << endl;
    return 0;
}

但明显能看出来此时使用了三个循环，此时时间复杂度较高，应考虑如何快速计算选0-k次中哪个结果最优，需要优化算法。下面是优化思路：
因为循环的嵌套是从i: 1-N, j: i-V计算的，所以在计算f[i,j]时，f[i, j-v]必然被算过（v代表i的体积，w代表i的重量）。f[i,j]与f[i, j-v]之间存在如下的联系：

那么可以看出两者的关系为

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];

int main(){
    cin >> n >> m;
    for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
    for(int i = 1; i <= n; i ++){
        for(int j = 0; j <= m; j++){
            f[i][j] = f[i - 1][j];
            if (j >= v[i]) f[i][j] = max(f[i][j], f[i][j-v[i]] + w[i]);
        }
    }
    cout << f[n][m] << endl;
    return 0;
}

进一步优化：可以把数组转化为一维数组，降低空间复杂度。因为每次计算新的f(i,j)只有第i-1行的当前元素和第i行的j以前元素有用，所以只用一个数组存f(i,j)不会出任何错，只保留j的参数，每次更新直接覆盖对应的j。
代码如下，其实就把上面的代码的f的所有第一个参数删掉：

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];

int main(){
    cin >> n >> m;
    for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
    for(int i = 1; i <= n; i ++){
        for(int j = 0; j <= m; j++){
            // f[j] = f[j]; 这行默认完成了，直接删掉
            if (j >= v[i]) f[j] = max(f[j], f[j-v[i]] + w[i]);
        }
    }
    cout << f[n][m] << endl;
    return 0;
}

多重背包问题

多重背包问题是每种物品的个数有限制，基础暴力做法和完全背包问题的暴力做法几乎一样，只是累积的上限不一样，即固定的个数限制。
但是在考虑相同的优化算法时，发现根据f[i,j-v]无法求得f[i,j]的最大值，因为若最大值等于其最后一项，则无法知道前面的最大值，而需要重新计算。(如下图所示)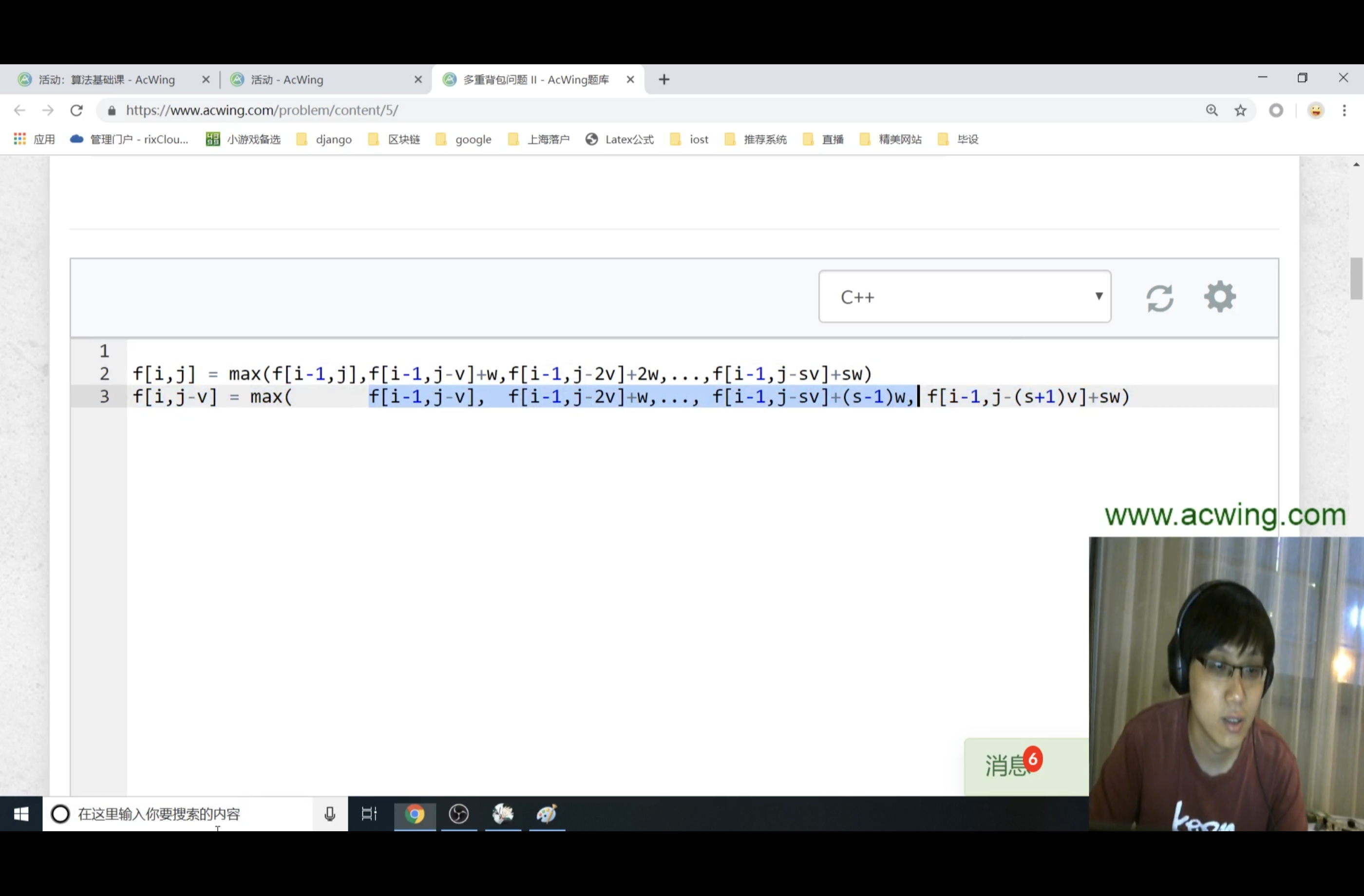

此时需要新的计算方法，先需要理解下面的数学原理：

则最终的代码：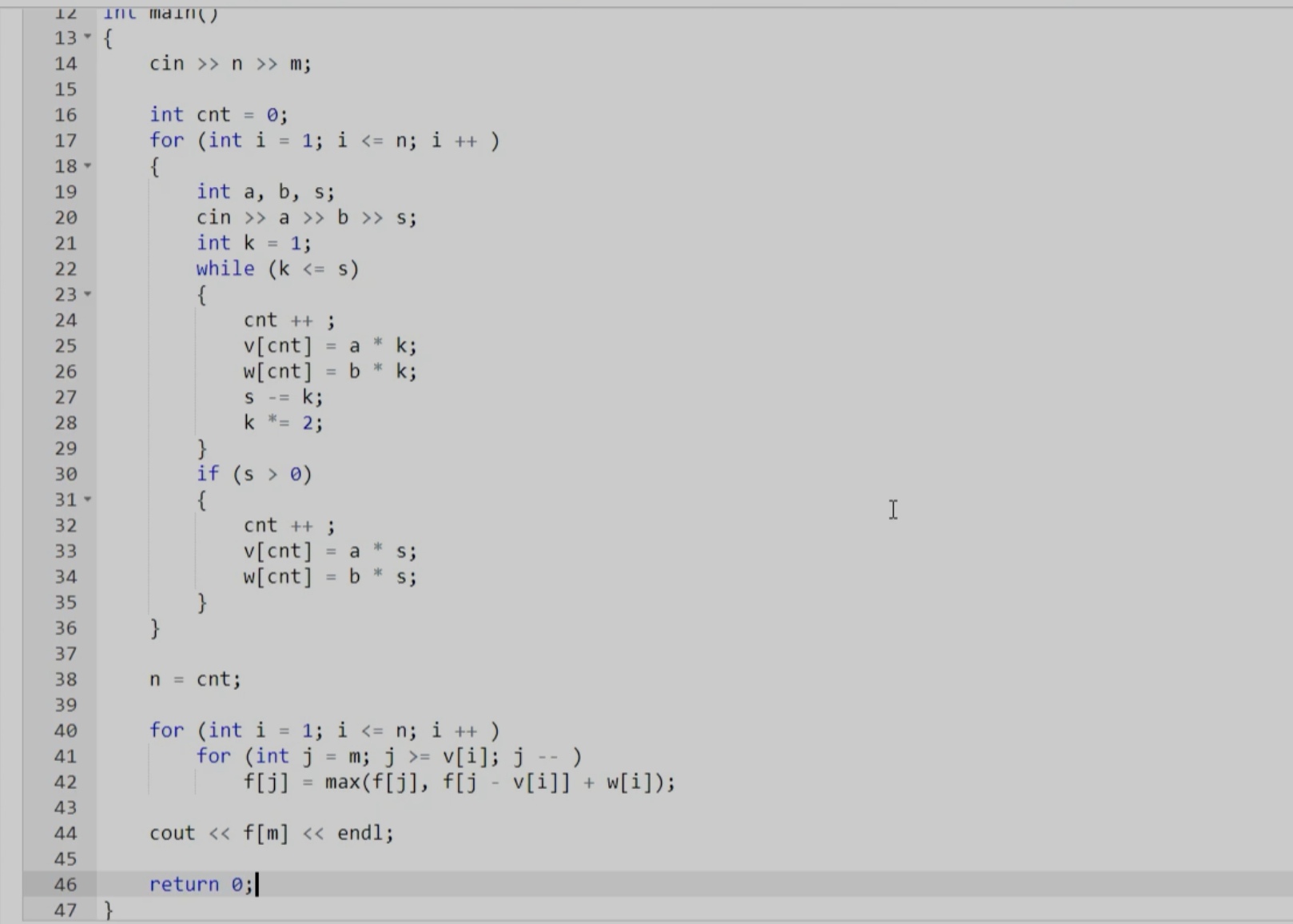

每组物品读入之后，在22-29行按照上面的数学原理拆分为2的幂次，用cnt记录现在的添加物品数量（最后一组直接使用s，而不是下一个2的幂次）。然后转化为01背包问题直接计算即可。