线性DP：递推方程有明显的线性的顺序。
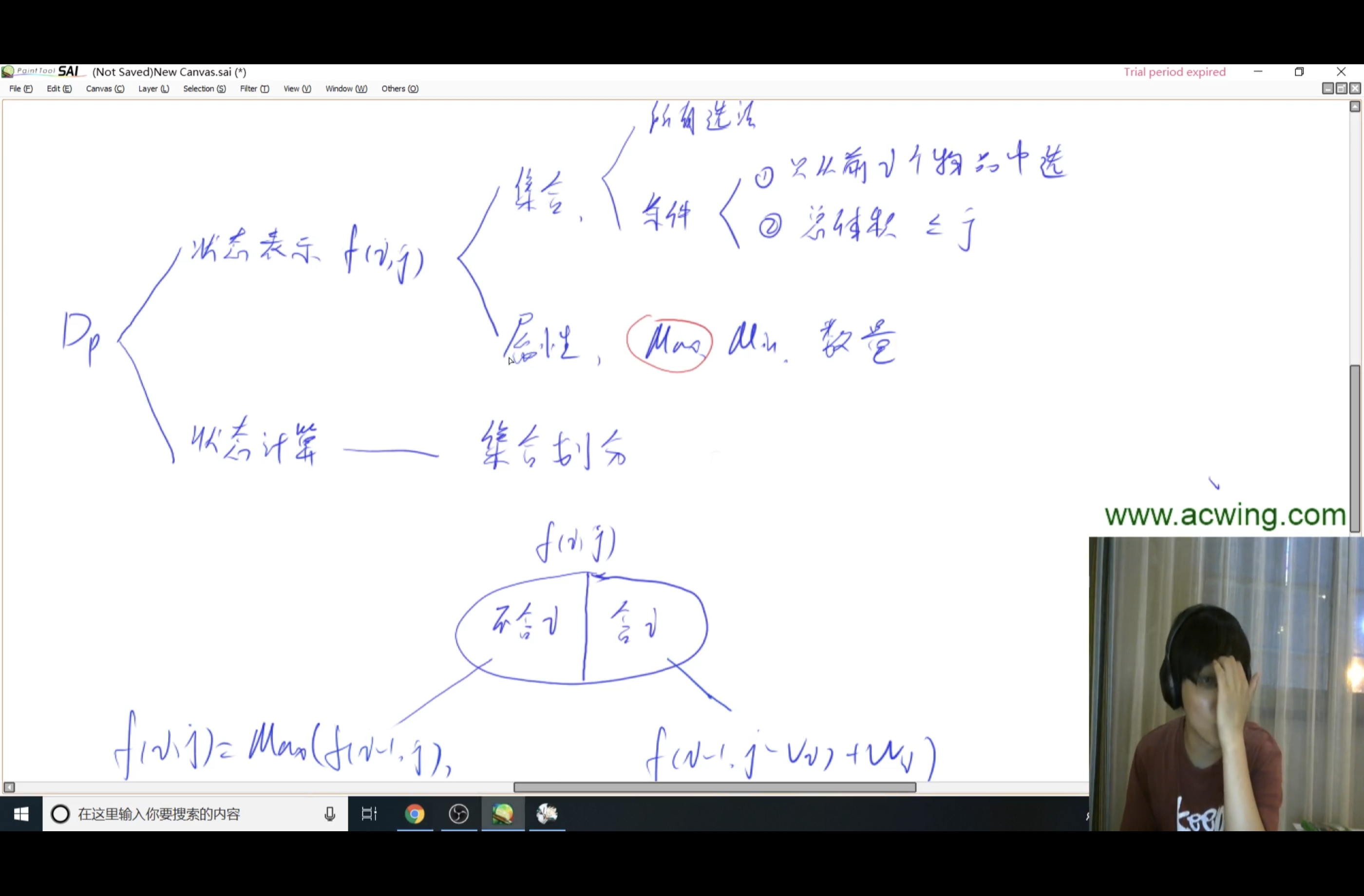
考虑两个问题：如何状态表示（集合+属性）、如何状态计算（划分状态转移集合）
T1：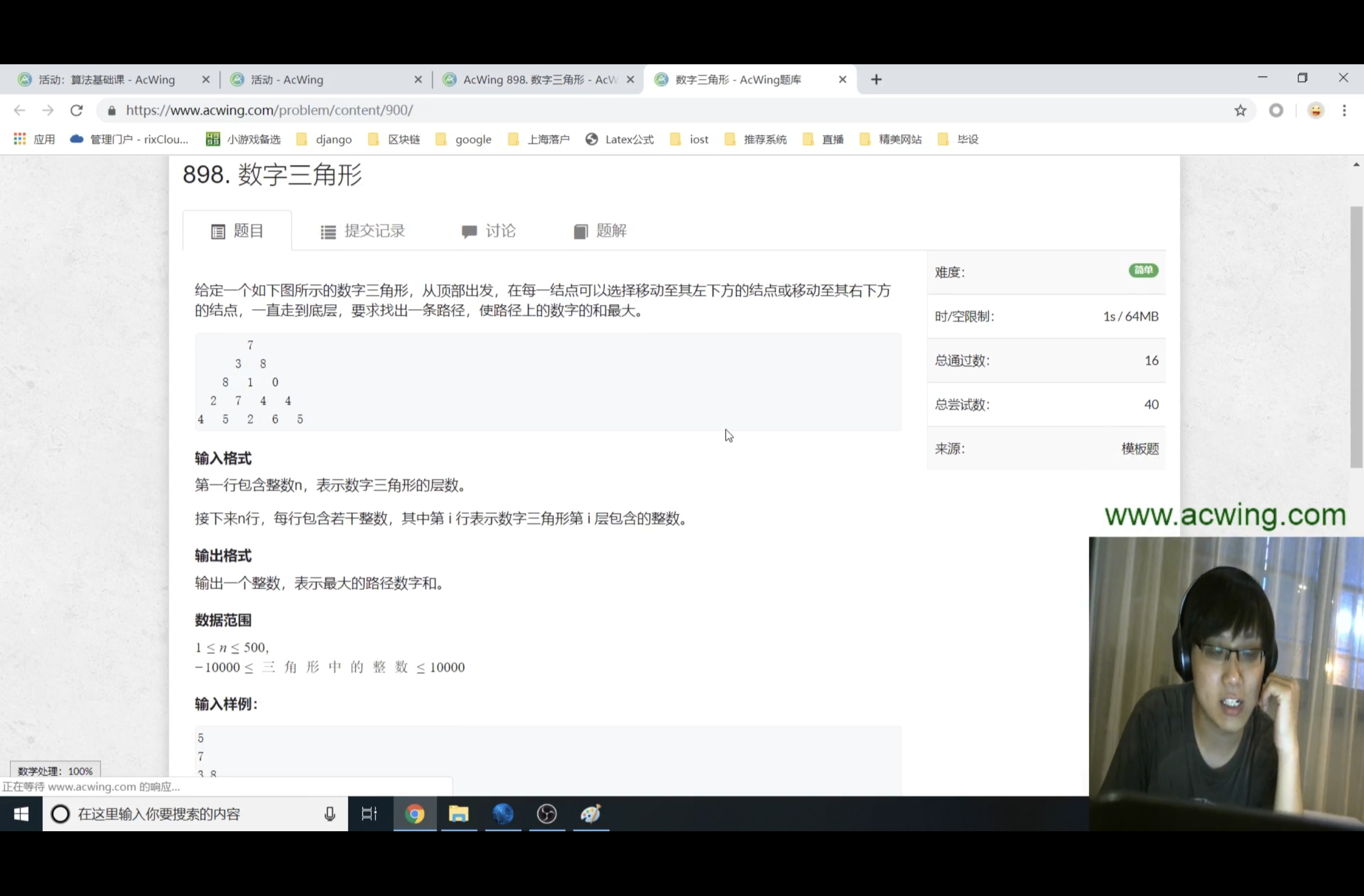

状态表示： 记录所有从起点走到(i,j)的路径中的路径数字之和的最大值。
状态计算：f[i,j] = max(f[i-1][j], f[i-1][j-1]) + a[i,j]
需要注意需要把f[i,j]初始化为极小值，避免算到三角形右边的元素。

T2：最长上升子序列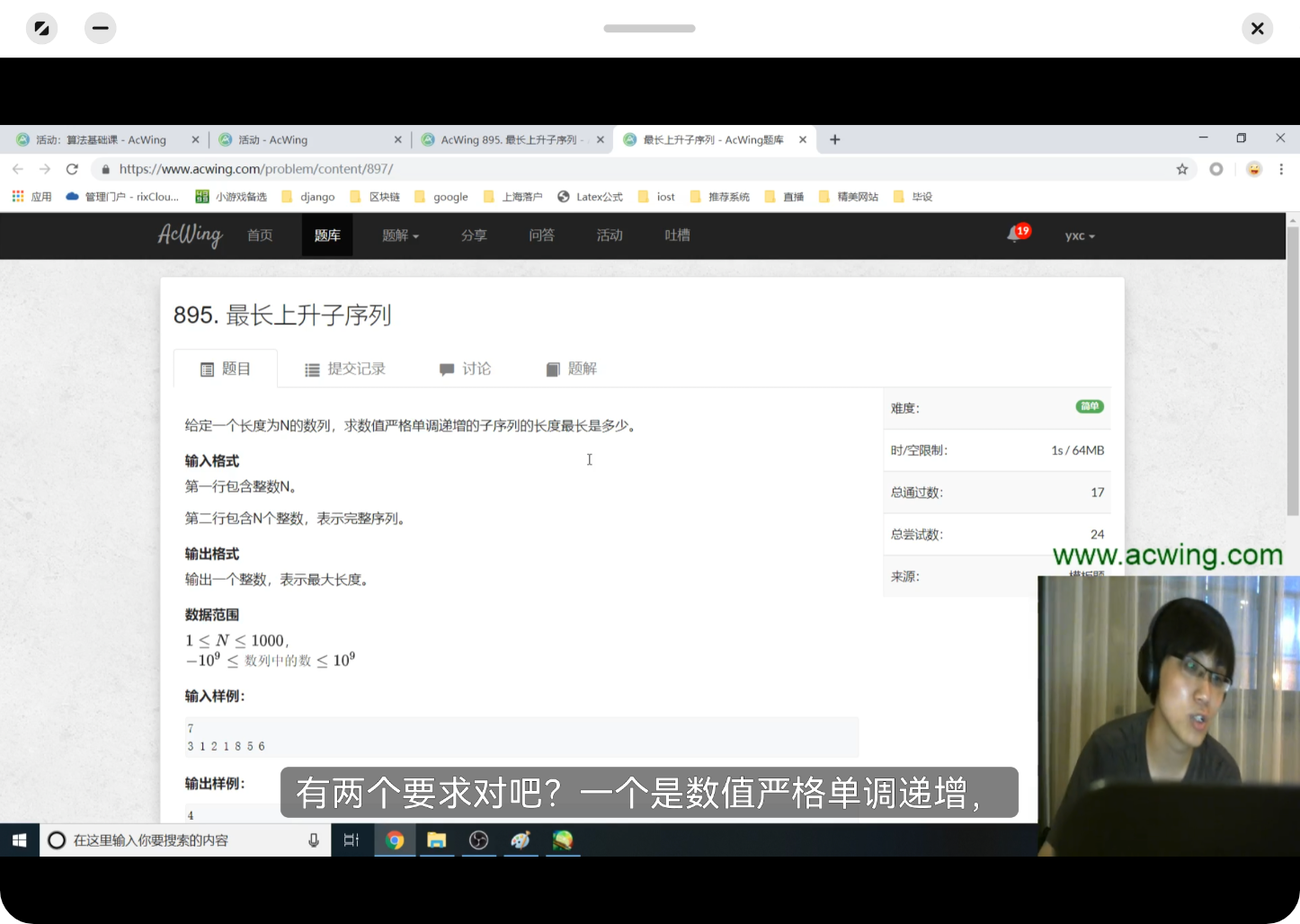

状态表示：使用一维数组，f[i]表示以第i个数结尾的上升子序列的长度的最大值。
状态计算：计算f[i]，去看倒数第二个数是哪个数，共i种可能，以编号1、2、3、……、i-1结尾或原本没有数（记为0）。每个循环先看是否满足上升的条件，若满足，则这个f[i]_j = f[j]+1，最后计算一个最大的f[i]_j就得出了f[i]的值。
时间复杂度计算：状态数量 × 转移的数量。此时是$n^2$。

#include <iostream>
#include <algorithm>

using namespace std;

int n;
int a[N], f[N];

int main(){
    scanf(“%d”, &n);
    for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
    for (int i = 1; i <= n; i++){
        f[i] = 1; //先全部赋值为1，只有a[i]一个数
        for(int j = 1; j < i; j++)
            if (a[j] < a[i])
                f[i] = max(f[i], f[j] + 1);
    }
    int res = 0;
    for(int i = 1; i <= n; i++) res = max(res, f[i]);
    printf("%d\n", res);
    return 0;
}

如何保存最长序列？
创建一个数组g[i]，存储每个转移是怎么转移过来的（记录上一个状态的id，也就是找f[i,j]最大值时找到的位置）。

阅读全文

本章主要介绍动态规划的常用思路，并介绍了背包问题里面的01背包、多重背包的解题思路和代码

01背包

01背包问题为：给定背包总体积，给N个物品，每个物品有一个体积和重量，只能用一次或不用，问最大重量是多少？
下面是思路，定义函数f(i,j)代表：仅包含前i个物品且总体积小于等于j的背包的最大价值是多少，故最终需要的结果是f(N,V)。
初始时把所有值都设为0，且i或j等于0的本身值就为0。
对于一个新的状态f(i,j)，可能的值有下面两种可能，如果包含i，则答案为f(i-1，j-vi) + wi；如果不包含i，则为f(i-1,j)。这两个值取最大值就可以算出f(i,j)。

代码：

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N][N];

int main(){
    cin >> n >> m;
    for(int i=1; i <= n; i++) cin >> v[i] >> w[i];
    for(int i=1; i <= n; i++)｛
        for(int j = 1; j <= m; j++){
            f[i][j] = f[i-1][j];
            if(j >= v[i]) f[i][j] = max(f[i][j], f[i-1][j-v[i]] + w[i]);
        }
    ｝
    cout << f[n][m] << endl;
}

阅读全文