北航软院算法 23级C7 题解

主播想要练习一下，故花了两个小时模拟了一下23级的C7赛

特意买了个学校机房同款包浆古董慢回弹键盘

A 选择题

第1题

KMP算法的提出者是哪几位___。

• A. D.E.Knuth
• B. J.H.Morris
• C. V.R.Pratt
• D. htunK.E.D
• E. sirroM.H.J
• F. ttarP.R.V

第2题

n个节点（1,...,n）的BST的不同形态数满足___。

• A.
  $$\Omega\left(\frac{4^n}{n^{\frac{3}{2}}}\right)$$
• B.
  $$O\left(\frac{4^n}{n^{\frac{3}{2}}}\right)$$
• C.
  $$\omega(1)$$
• D.
  $$o(4^n)$$

第3题

以下说法正确的是___。

• A. 均摊分析主要包括聚合分析、记账分析和势能分析。
• B. 均摊分析考虑的是最好情况下的平均时间
• C. 期末考试可以使用共享文档
• D. 使用聚合分析能够分析出Graham's Scan算法的复杂度是 $O(nh)$

第4题

以下说法正确的是___。

• A. Graham's Scan的时间复杂度是 $O(n\lg n)$
• B. Jarvis's March的时间复杂度是 $O(n\lg n)$
• C. Prim算法是贪心思想的应用
• D. 对于网络流图上的容量 $c$ 和流量 $f$，有 $0 \le c(u,v) \le f(u,v)$。

第5题

对于含有负权边但不含负环的图，以下哪些算法能求出正确的最短路？___。

• A. Floyd
• B. Dijkstra
• C. Bellman Ford
• D. 以上都不对

代码

纯蒙，不一定对

#include <bits/stdc++.h>

using namespace std;

int main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    cout << "ABC" << '\n';
    cout << "ABCD" << '\n';
    cout << "A" << '\n';
    cout << "AC" << '\n';
    cout << "AC" << '\n';
    return 0;
}

B 比赛裁判

猫猫是比赛的裁判！

总共有 $n$ 位选手参加比赛，这些选手编号为 $1,2,\dots,n$。

猫猫宣布，比赛分为 $k$ 轮，在第 $i$ 轮中淘汰编号是 $i+1$ 的倍数的选手。

每轮中分别淘汰了多少位选手呢？

输入

本题测试点包含多组数据。
第一行，一个正整数 $T$（$1 \le T \le 10$），表示数据组数。

对于每组数据：
一行，两个整数 $n,k$（$2 \le n \le 10^3,\ 1 \le k < n$）。

输出

对于每组数据：
输出一行，$k$ 个整数。第 $i$ 个整数表示第 $i$ 轮中淘汰的选手数量。

输入样例

2
5 3
7 6

输出样例

2 1 0
3 1 0 1 0 1

代码

#include <bits/stdc++.h>

using namespace std;

int main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    int n;
    int t;
    int k;
    cin >> t;
    while(t--){
        cin >> n >> k;
        vector<int> v(n+3, 0);
        for(int i = 1; i <= k ;i++){
            int sum = 0;
            for(int j = 1; j <= n; j++){
                if(v[j]==0 && j%(i+1)==0){
                    sum++; v[j] = 1;
                }
            }
            cout << sum << ' ';
        }
        cout << '\n';
    }
    return 0;
}

C 车厢调度

题目描述

猫猫是火车站调度员！

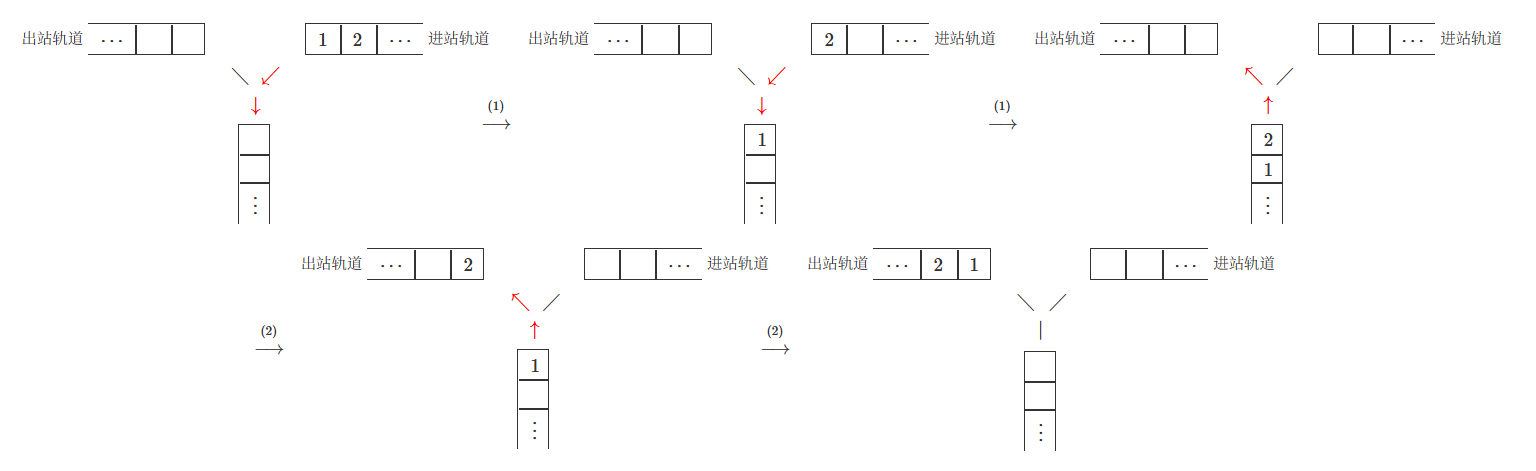
猫猫需要利用一条 $Y$ 形轨道调度火车车厢，$Y$ 形轨道右侧连接进站轨道，左侧连接出站轨道。

具体来说，火车停靠在进站轨道，共有 $n$ 节车厢，车厢的编号依次是 $1,2,\dots,n$。最终火车需要停靠在出站轨道，并且车厢编号依次为 $p_1,p_2,\dots,p_n$。

利用 $Y$ 形轨道，猫猫每次可以进行以下两种操作之一：

1. 将当前进站轨道最靠近道岔的车厢移入 $Y$ 形轨道。
2. 将 $Y$ 形轨道最靠近道岔的车厢移入出站轨道。

例如按以下方式，可以将进站轨道停靠的车厢 $1,2$，变为出站轨道停靠的车厢 $2,1$。

猫猫想知道，能否只通过这两种操作将火车按照车厢 $p_1,p_2,\dots,p_n$ 的顺序停靠在出站轨道呢？

输入

本题测试点包含多组数据。

第一行，一个正整数 $T$（$1 \le T \le 20$），表示数据组数。

对于每组数据：

• 第一行，一个正整数 $n$（$1 \le n \le 10^4$），表示车厢数量。
• 第二行，$n$ 个互不相同的正整数 $p_1,\dots,p_n$（$1 \le p_i \le n$），表示目标车厢顺序。

输出

对于每组数据：

输出一行，若只通过给出的两种操作能将车厢调度为目标顺序，则输出 YES；否则输出 NO。

输入样例

3
2
2 1
4
1 3 2 4
4
3 1 2 4

输出样例

YES
YES
NO

提示

样例中的第一组数据即是题目描述中给出的例子。

代码

#include <bits/stdc++.h>

using namespace std;

int main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    int t, n;
    cin >> t;
    while(t--){
        cin >> n;
        stack<int> s1;
        stack<int> s2;
        stack<int> s3;
        for(int i = n; i >= 1; i--){
            int v;
            cin >> v;
            s1.push(v);
        }
        for(int i = n; i >= 1; i--){
            if(!s2.empty() && s2.top() == i){
                s2.pop();
                s3.push(i);
                continue;
            }
            else{
                while(!s1.empty()){
                    int top = s1.top(); s1.pop();
                    if(top == i){
                        s3.push(i); goto nxt;
                    }else{
                        s2.push(top);
                    }
                }
                cout << "NO\n";goto nnxt;
            }
            nxt:{}
        }
        cout << "YES\n";
        nnxt:{}
    }
    return 0;
}

D 数列配对

题目描述

猫猫正在与算法激烈搏斗！

猫猫遇到了一道算法问题，并找到了你求助。问题是这样的：

小 A 手上有 $n$ 个整数 $a_1,a_2,\dots,a_n$，小 B 手上有 $n$ 个整数 $b_1,b_2,\dots,b_n$。猫猫每次可以从小 A 手上拿走一个整数 $a_{p_i}$，并从小 B 手上拿走一个整数 $b_{q_i}$，如果 $a_{p_i} < b_{q_i}$ 则能成功将这两个整数配成一对，否则无法配对。

小 A 和小 B 手上的整数最多能配成多少对呢？

输入

第一行，一个正整数 $n$（$1 \le n \le 10^5$）。

第二行，$n$ 个整数 $a_1,a_2,\dots,a_n$（$0 \le a_i \le 10^9$）。

第三行，$n$ 个整数 $b_1,b_2,\dots,b_n$（$0 \le b_i \le 10^9$）。

输出

输出一行，一个整数，表示最多配对数量。

输入样例

5
1 5 3 4 7
0 2 3 6 6

输出样例

3

提示

样例中可以将小 A 的 $1,4,5$ 分别与小 B 的 $3,6,6$ 配对，可以证明这种方案有最多的配对数量。

代码

#include <bits/stdc++.h>

using namespace std;

int a[100009], b[100009];

int main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    int n;
    cin >> n;
    for(int i = 0; i<n; i++){
        cin >> a[i];
    }
    for(int i = 0; i<n; i++){
        cin >>b[i];
    }
    sort(a, a+n);
    sort(b, b+n); int i = 0; int j = 0;
    int sum = 0;
    while(i < n && j < n){
        if(a[i] < b[j]){
            sum++;
            i++; j++;
        }else j++;
    }
    cout << sum;
    return 0;
}

E 复习安排

题目描述

猫猫即将开始紧张刺激的考期！

考期总共有 $n$ 天，猫猫有 $k$ 门课需要考试。对于第 $i$ 门课，如果想顺利通过考试，必须在考期的第 $l_i$ 天到第 $r_i$ 天全身心投入这门课的复习，不能复习其他课程，否则就会挂科。

猫猫最多能通过多少门课的考试？

输入

本题测试点包含多组数据。

第一行，一个正整数 $T$（$1 \le T \le 5$），表示数据组数。

对于每组数据：

• 第一行，两个正整数 $n,k$（$1 \le n \le 10^5,\ 1 \le k \le n$），分别表示考期天数和课程数。
• 接下来 $k$ 行，每行两个正整数 $l_i,r_i$（$1 \le l_i \le r_i \le n$），表示通过第 $i$ 门课的考试所需的复习起止天数。

输出

对于每组数据：

输出一行，一个整数，表示最多能通过的考试数量。

输入样例

2
8 4
1 1
2 4
4 5
6 8
5 3
1 3
2 4
3 5

输出样例

3
1

代码

#include <bits/stdc++.h>

using namespace std;

int n, k, t;
int sum = 0;
pair<int, int> lesson[100009]; // r, l

int main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    cin >> t;
    while(t--){
        cin >> n >> k;
        for(int i = 0; i<k; i++){
            cin >> lesson[i].second >> lesson[i].first;
        }
        sum = 0;
        
        sort(lesson, lesson+k);
        int last = -2e9;
        for(int i = 0 ; i< k;i++){
            pair<int, int> x = lesson[i];
            // cout << x.second << x.first << '\n';
            if(x.second > last){
                sum++;
                last = x.first;
                
            }
        }
        cout << sum << '\n';
    }
    return 0;
}

F 数字魔法

题目描述

猫猫学了一个神奇的数字魔法！Abracadabra!

猫猫有一个长度为 $n$ 的数列 $a_1,\dots,a_n$，每次可以对数列施展以下数字魔法：

• 选择数列中相邻两个数 $x,y$，将数列中这两个数替换为一个数 $|x-y|$。

数列每次被施展魔法之后长度都会减少 $1$，因此 $n-1$ 次魔法之后数列中只剩一个数。由于每次可以选择数列中不同位置施展魔法，不同方案中最后剩下的数不一定相同。猫猫想知道所有可能情况中，最后剩下的数的最小值和最大值分别是多少。

输入

第一行，一个整数 $n$（$1 \le n \le 50$），表示数列长度。
第二行，$n$ 个整数 $a_1,\dots,a_n$（$0 \le a_i \le 50$）。

输出

一行，两个整数，分别表示所有可能情况中最后剩下的数的最小值和最大值。

输入样例

3
2 3 4

输出样例

1 3

提示

对于样例，总共有两种不同的施展魔法的方案。第一种方案是：

• $[2,3,4]\to[2,1]$
• $[2,1]\to[1]$

第二种方案是：

• $[2,3,4]\to[1,4]$
• $[1,4]\to[3]$

因此最后剩下的数最小为 $1$，最大为 $3$。

代码

#include <bits/stdc++.h>

using namespace std;

int dp[56][56][56];

int a[56];

int main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    int n;
    cin >> n;
    for(int i = 1; i <= n; i++){
        cin >> a[i];
        dp[i][i][a[i]] = 1;
    }
    for(int l = 2; l <= n; l++){
        for(int i = 1; i <= (n - l + 1); i++){
            int left = i; int right = i + l - 1;
            int mid = left;
            while(mid < right){
                for(int w1 = 0; w1 <= 50; w1++)
                    for(int w2 = 0; w2 <= 50; w2++)
                        if(dp[left][mid][w1]!=0 && dp[mid + 1][right][w2]!=0) dp[left][right][abs(w1 - w2)]++;
                mid++;
            }
        }
    }
    int mmin = 114514, mmax = -114514;
    for(int i = 0; i <= 50; i++){
        if(dp[1][n][i] > 0){ mmin = min(mmin, i); mmax = max(mmax, i);}
    }
    cout << mmin << ' ' << mmax;
    return 0;
}

G 收作业！

题目描述

猫猫是《猫科动物野外生存指南》课程的助教！

课程共有 $n$ 位小猫同学，这些同学依次以 $1,\dots,n$ 编号，助教以 $n+1$ 编号。同学们需要将作业交给助教，但由于很多同学不认识助教，所以会委托它们认识的其他同学转交作业。

具体来说，这 $n+1$ 只猫之间共有 $m$ 对猫相互认识。在第 $i$ 对关系 $(u_i,v_i,c_i)$ 中，编号为 $u_i$ 的猫与编号为 $v_i$ 的猫互相认识，并且两只猫之间传递作业的代价是 $c_i$。除了给定关系之外，任意两只猫之间互相不认识。同学们通过进行多次以下操作，将作业交给助教：

• 选定一对关系 $(u_i,v_i,c_i)$，其中一只猫将它手上的所有作业传递给另一只猫，这一操作的代价是 $c_i$。

最终助教手上有所有同学的作业时结束操作。同学们想知道，将所有同学的作业交给助教需要的最小代价和是多少？

输入

第一行，两个正整数 $n,m$（$1 \le n \le 10^5,\ 1 \le m \le 2\times 10^5$），分别表示同学数量，以及关系数量。

接下来 $m$ 行，每行三个正整数 $u_i,v_i,c_i$（$1 \le u_i, v_i \le n+1,\ 1 \le c_i \le 10^6$），分别表示互相认识的猫的编号，以及这两只猫之间传递作业的代价。

保证每只猫都能将作业交给助教。

输出

一行，一个正整数，表示交作业所需的最小代价和。

输入样例

3 5
1 2 3
1 3 2
3 2 4
3 4 1
2 4 1

输出样例

4

代码

最小生成树

#include <bits/stdc++.h>

using namespace std;

int n, m;
const int N = 100005;
const int M = 400005;
const int INF = 0x3f3f3f3f;
struct Edge{
    int to, w, next;
}e[M];

int cnt_E = 0;
int head[N];

void init(){
    memset(head, -1, sizeof(head));
}

void addEdge(int x,int y, int w){
    e[cnt_E].next = head[x];
    e[cnt_E].to = y;
    e[cnt_E].w = w;
    head[x] = cnt_E++;
}

typedef pair<int, int> PII;

long long prim(int n, int start){
    long long dis[N];
    bool vis[N];
    memset(dis, 0x3f, sizeof(dis));
    memset(vis, 0, sizeof(vis));
    priority_queue<PII, vector<PII>, greater<PII>> q;
    dis[start] = 0;
    q.push({0, start});
    long long res = 0;
    long long cnt = 0;
    while(!q.empty()){
        long long d= q.top().first;
        long long u = q.top().second;
        q.pop();
        if(vis[u]) continue;
        vis[u] = true;
        res+=d;
        cnt++;
        for(int i = head[u]; i!=-1; i = e[i].next){
            long long v= e[i].to;
            long long w= e[i].w;
            if(!vis[v] && w < dis[v]){
                dis[v] = w;
                q.push({dis[v], v});
            }
        }
    }
    return res;
}

int main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    cin >> n >> m;
    init();
    for(int i = 1; i <= m; i++){
        int uu, vv ,cc;
        cin >> uu >> vv>>cc;
        addEdge(uu, vv, cc);
        addEdge(vv, uu ,cc);
    }
    cout << prim(n+1, n+1);
    return 0;
}

H 路线规划

题目描述

猫猫是幼儿园园长！

幼儿园的小猫们准备前往公园秋游。城里共有 $n$ 个路口，幼儿园位于 $1$ 号路口，公园位于 $n$ 号路口。$m$ 条单向道路连接着这些路口，从 $u_i$ 号路口可以沿第 $i$ 条单向道路前往 $v_i$ 号路口。

猫猫注意到，如果有两只小猫前往公园的路线经过了相同的道路，那么它们会在这条道路上打架。需要注意的是，经过相同的路口不会打架。

猫猫想知道，在不发生打架的前提下，最多能有多少只小猫前往公园呢？

输入

第一行，两个正整数 $n,m$（$1 \le n \le 500,\ 1 \le m \le 10000$），分别表示路口数量与单向道路的数量。

接下来 $m$ 行，每行两个整数 $u_i,v_i$（$1 \le u_i, v_i \le n$），表示一条从 $u_i$ 到 $v_i$ 的单向道路。

注意可能有多条不同的道路连接 $u_i$ 与 $v_i$。

输出

一行，一个整数，表示在不发生打架的前提下，最多能有前往公园的小猫数量。

输入样例

4 5
1 3
3 4
3 2
1 2
2 4

输出样例

2

提示

在样例中，第一只小猫沿路线 $1 \to 2 \to 4$ 前往公园，第二只小猫沿路线 $1 \to 3 \to 4$ 前往公园。

代码

最大流

#include <bits/stdc++.h>

using namespace std;

int n, m;
const int N = 505;
const int M = 5005;
const int INF = 0x3f3f3f3f;
struct Edge{
    int to, w, next;
}e[M];

int cnt_E = 0;
int head[N];

void init(){
    memset(head, -1, sizeof(head));
}

int dep[N];
int cur[N];

void addEdge(int x,int y, int w){
    e[cnt_E].next = head[x];
    e[cnt_E].to = y;
    e[cnt_E].w = w;
    head[x] = cnt_E++;
}

bool bfs(int S, int T){
    memset(dep, -1, sizeof(dep));
    queue<int> q;
    dep[S] = 0;
    q.push(S);
    memcpy(cur, head, sizeof(head));

    while(!q.empty()){
        int u = q.front();
        q.pop();
        for(int i = head[u]; i != -1; i = e[i].next){
            int v= e[i].to;
            int w = e[i].w;
            if(w > 0 && dep[v] == -1){
                dep[v] = dep[u] + 1;
                q.push(v);
            }
        }
    }
    return dep[T] != -1;
}

int dfs(int u, int limit, int T){
    if(u == T || limit == 0) return limit;
    int flow = 0;
    for(int &i = cur[u]; i!=-1; i = e[i].next){
        int v = e[i].to;
        int w = e[i].w;
        if(dep[v] == dep[u] + 1 && w > 0){
            int f = dfs(v, min(limit, w), T);
            if(f > 0){
                e[i].w -= f;
                e[i ^1].w += f;
                flow += f;
                limit -= f;
                if(limit == 0) break;
            }
        }
    }
    return  flow;
}

int dinic(int S, int T){
    int max_flow = 0;
    while(bfs(S,T)){
        max_flow += dfs(S, INF , T);
    }
    return max_flow;
}

int main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    cin >> n >> m;
    init();
    for(int i = 1; i <= m ;i++){
        int ui, vi;
        cin >> ui >> vi;
        addEdge(ui, vi, 1);
        addEdge(vi, ui, 0);
    }
    cout << dinic(1, n) << endl;
    return 0;
}

I 数列询问

题目描述

猫猫在书上看到了一个神奇的名词——卷积！

猫猫有两个数列，一个是长度为 $n$ 的数列 $a_1,a_2,\ldots,a_n$，另一个是长度为 $m$ 的数列 $b_1,b_2,\ldots,b_m$。

猫猫有 $q$ 个询问。在第 $i$ 个询问中，猫猫给出正整数 $k$，你需要回答下式的值：

其中 $1\le i\le n,\ 1\le j\le m$。

输入

第一行，三个正整数 $n,m,q$（$1\le n,m\le 10^5,\ 1\le q\le 2\times 10^5$），分别表示数列 $\{a\}$ 的长度、数列 $\{b\}$ 的长度，以及询问个数。

第二行，$n$ 个非负整数 $a_1,\ldots,a_n$（$0\le a_i\le 10$）。

第三行，$m$ 个非负整数 $b_1,\ldots,b_m$（$0\le b_i\le 10$）。

接下来 $q$ 行，每行一个正整数 $k$（$1\le k\le 2\times 10^5$），表示一个询问。

输出

输出共 $q$ 行。对于每个询问，输出一行，一个整数，表示

的值。

输入样例

3 4 2
1 2 3
0 1 2 3
3
5

输出样例

1
10

提示

对于样例中的第一个询问，答案为 $a_1b_2+a_2b_1=1$。

对于样例中的第二个询问，答案为 $a_1b_4+a_2b_3+a_3b_2=10$。

代码

#include <bits/stdc++.h>

using namespace std;

const double PI = acos(-1.0);
const int MAXN = 262144+5;

struct Complex{
    double x, y;
    Complex(double x = 0, double y = 0): x(x), y(y){}
    Complex operator+(const Complex &b) const {return Complex(x+b.x, y+b.y);}
    Complex operator-(const Complex &b) const {return Complex(x- b.x, y-b.y);}
    Complex operator*(const Complex &b) const {return Complex(x*b.x-y*b.y, x*b.y+y*b.x);}
};

void fft(Complex *a, int n, int type){
    static int rev[MAXN];
    static int last_n = 0;
    if(n!= last_n) {
        last_n = n;
        int bit = 0;
        while((1<<bit)<n) bit++;
        for(int i = 0; i < n; i++){
            rev[i] = (rev[i >> 1] >> 1) |((i & 1) << (bit - 1));
        }

    }
    for(int i = 0; i < n; i++){
        if(i < rev[i]) swap(a[i], a[rev[i]]);
    }
    for(int mid = 1; mid < n; mid <<= 1){
        Complex wn(cos(PI/mid),type*sin(PI/mid));
        for(int R = mid << 1, j = 0; j<n; j+= R){
            Complex w(1,0);
            for(int k = 0; k < mid; k++, w = w*wn){
                Complex x = a[j + k];
                Complex y = w * a[j + k + mid];
                a[j + k] = x + y;
                a[j + k + mid] = x - y;
            }
        }
    }
    if(type == -1){
        for(int i = 0; i < n; i++) a[i].x /= n;
    }
}

int n, m , q;
Complex a[MAXN], b[MAXN];

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);
    cin >> n >> m >> q;
    for(int i = 0; i < n; i++) cin >> a[i].x;
    for(int i = 0; i < m; i++) cin >> b[i].x;
    n--; m--;
    int limit = 1;
    while(limit <= n + m) limit <<= 1;
    fft(a, limit, 1);
    fft(b, limit, 1);
    for(int i = 0; i < limit; i++) a[i] = a[i]*b[i];
    fft(a, limit, -1);
    while(q--){
        int k;
        cin >> k;
        cout << (int)(a[k - 2].x + 0.5) << '\n';
    }
}

J 优秀数对

题目描述

猫猫发现了好多字符串！

猫猫有 $n$ 个仅包含小写英文字母的字符串 $S_1,\ldots,S_n$。如果字符串 $S_i$ 是 $S_j$ 的子串（$1\le i,j\le n$），那么称有序对 $(i,j)$ 是优秀的。对于 $1\le i,j\le n$，$(i,j)$ 中总共有多少个优秀的数对呢？

称字符串 $S_i$ 是 $S_j$ 的子串，当且仅当从 $S_j$ 删去某个可以为空的前缀与某个可以为空的后缀之后，可以得到 $S_i$。

例如 $abc$ 是 $dabc$ 的子串，但 $abc$ 不是 $adbd$ 的子串。

输入

第一行，一个正整数 $n$（$1\le n\le 500$），表示字符串的数量。

接下来 $n$ 行，每行一个仅包含小写英文字母的字符串 $S_i$。

保证所有字符串长度之和不超过 $5\times 10^4$。

输出

一行，一个整数，表示优秀数对的数量。

输入样例

4
ab
ab
abab
dabc

输出样例

10

提示

样例中优秀数对有 $(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,3),(4,4)$，共有 $10$ 对。

代码

#include <bits/stdc++.h>

using namespace std;

int n;

string s[509];

long long ans = 0;

bool cmp(string a, string b){
    return a.length() < b.length();
}

int main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    cin >> n;
    for(int i = 0; i < n; i++){
        cin >> s[i];
    }
    sort(s, s+n, cmp);
    for(int i = 0; i < n; i++){
        ans += 1;
        for(int j = i + 1; j < n; j++){
            if(s[j].find(s[i]) != string::npos){
                ans ++;
                //cout << i << ' ' << j << '\n';
                if(s[j].length() == s[i].length()) ans++;
            }
        }
    }
    cout << ans;
    return 0;
}

K 再见七海

题目描述

猫猫即将踏上新的征程！

猫猫即将出海远航，但不幸的是猫猫不会游泳。

在 $\mathbb{R}^2$ 海洋上漂浮着 $n$ 个浮标，第 $i$ 个浮标的坐标是 $(x_i,y_i)$。海浪把这些浮标冲得很分散，因此这些浮标的坐标都是随机的。

猫猫想从这些浮标中选择三个浮标搭建救生筏，所以希望这三个浮标之间两两以线段连接之后，所形成的三角形面积尽可能的大。

最大的三角形面积是多少呢？

输入

第一行，一个正整数 $n$（$3\le n\le 10^5$），表示浮标数量。

接下来 $n$ 行，每行两个整数 $x_i,y_i$（$0\le x_i,y_i\le 10^6$），表示浮标的坐标。

保证没有多个浮标坐标相同。保证坐标均是随机生成的。

输出

一行，一个保留一位的实数，表示浮标形成的三角形的最大面积。

输入样例

5
0 0
1 0
0 1
1 2
2 1

输出样例

1.5

代码

计算几何题，还没做出来